
【题目】为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩(![]() 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分数段(分) | 频数(人) | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |

(1)填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)将频数分布直方图补充完整;
(3)该校对成绩为![]() 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为
的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为![]() ,请你估算全校获得二等奖的学生人数;
,请你估算全校获得二等奖的学生人数;
(4)结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.
科目:初中数学 来源: 题型:
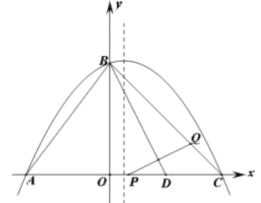
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的顶点坐标;
求这条抛物线的顶点坐标;
![]() 已知
已知![]() (点
(点![]() 在线段
在线段![]() 上),有一动点
上),有一动点![]() 从点
从点![]() 沿线段
沿线段![]() 以每秒
以每秒![]() 个单位长度的速度移动:同时另一个点
个单位长度的速度移动:同时另一个点![]() 以某一速度从点
以某一速度从点![]() 沿线段
沿线段![]() 移动,经过
移动,经过![]() 的移动,线段
的移动,线段![]() 被
被![]() 垂直平分,求
垂直平分,求![]() 的值;
的值;
![]() 在
在![]() 的情况下,抛物线的对称轴上是否存在一点
的情况下,抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的值最小?若存在,请求出点
的值最小?若存在,请求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
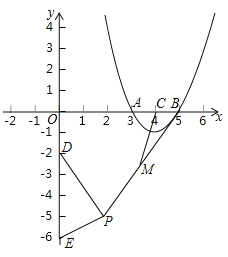
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民消费价格指数是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.据统计,从2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率如下图所示:

根据上图提供的信息,下列推断中不合理的是( )
A.2018年12月的增长率为0.0%,说明与2018年11月相比,全国居民消费价格保持不变
B.2018年11月与2018年10月相比,全国居民消费价格降低0.3%
C.2018年9月到2019年8月,全国居民消费价格每月比上个月的增长率中最小的是-0.4%
D.2019年1月到2019年8月,全国居民消费价格每月比上个月的增长率一直持续变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (
(![]() ).
).
(1)写出抛物线顶点的纵坐标 (用含a的代数式表示);
(2)若该抛物线与x轴的两个交点分别为点A和点B,且点A在点B的左侧,AB=4.
①求a的值;
②记二次函数图象在点A,B之间的部分为W(含点A和点B),若直线![]() (
(![]() )经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
)经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
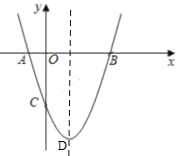
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线顶点为
,抛物线顶点为![]() ,下列四个结论:①无论
,下列四个结论:①无论![]() 取何值,
取何值,![]() 恒成立;②当
恒成立;②当![]() 时,
时,![]() 是等腰直角三角形;③若
是等腰直角三角形;③若![]() 则
则![]() ;④抛物线上有两点
;④抛物线上有两点![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②④B.②③④C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为国家级开发区的两江新区,大小公园星罗棋布,称为“百园之城”.该区2018年绿地总面积为2500万平方米,2020年绿地总面积将比2018年增加3500万平方米,人口比2018年增加50万人.这样,2020年该区人均绿地面积是2018年人均绿地面积的2倍.
(1)求2020年两江新区的人口数量;
(2)2020年起,为了更好地建设“一半山水一半城”的美丽新区,吸引外来人才落户两江新区,新区管委会在增加绿地面积的同时大力扩展配套水域面积.根据调查,2020年新区的配套水域面积为人均4平方米.在2020年的基础上,如果人均绿地每增加1平方米,人均配套水域将增加![]() 平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
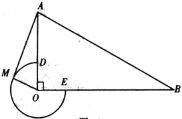
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
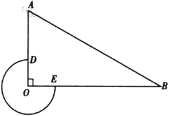
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②都是![]() 的正方形网格,每个小正方形的顶点叫做格点.
的正方形网格,每个小正方形的顶点叫做格点.![]() 的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)在图①中过点![]() 作
作![]() 面积两等分的射线.
面积两等分的射线.
(2)在图②中过点![]() 作所有将
作所有将![]() 面积分成1:2的两部分的射线.
面积分成1:2的两部分的射线.
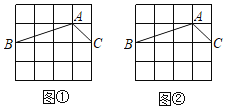
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com