
����Ŀ����Ϊ���Ҽ���������������������С�������岼����Ϊ����֮����������2018���̵������Ϊ2500��ƽ���ף�2020���̵����������2018������3500��ƽ���ף��˿ڱ�2018������50���ˣ�������2020������˾��̵������2018���˾��̵������2����
��1����2020�������������˿�������
��2��2020����Ϊ�˸��õؽ�����һ��ɽˮһ��������������������������˲��仧����������������ί���������̵������ͬʱ������չ����ˮ����������ݵ��飬2020������������ˮ�����Ϊ�˾�4ƽ���ף���2020��Ļ����ϣ�����˾��̵�ÿ����1ƽ���ף��˾�����ˮ������![]() ƽ���ף��˿�Ҳ����֮����5����������������2022����̵������������ˮ�������Ҫ��2020��Ļ���������75%����ô2022���˾��̵����Ҫ��2020�����Ӷ���ƽ���ף�
ƽ���ף��˿�Ҳ����֮����5����������������2022����̵������������ˮ�������Ҫ��2020��Ļ���������75%����ô2022���˾��̵����Ҫ��2020�����Ӷ���ƽ���ף�
���𰸡���1��2020�������������˿�����Ϊ300���ˣ���2��2022���˾��̵����Ҫ��2020������10ƽ���ף�
��������
��1����2020�������������˿�����Ϊx���ˣ�����2020������˾��̵������2018���˾��̵������2���з�ʽ�������x��ֵ�����鼴�ɣ�
��2����2022���˾��̵����Ҫ��2020������xƽ���ף���2022���˿�����5x���˾�����ˮ������![]() xƽ���ף�������������2020����̵����������ˮ�����������2022����̵������������ˮ�������Ҫ��2020��Ļ���������75%�з������x��ֵ���ɵô𰸣�
xƽ���ף�������������2020����̵����������ˮ�����������2022����̵������������ˮ�������Ҫ��2020��Ļ���������75%�з������x��ֵ���ɵô𰸣�
��1����2020�������������˿�����Ϊx���ˣ���2018���˿�����Ϊ(x-50)��
��2020������˾��̵������2018���˾��̵������2����
��![]() ��
��
��ã�x=300��
�����飺x=300��ԭ��ʽ���̵Ľ⣬�ҷ������⣬
��2020�������������˿�����Ϊ300���ˣ�
��2����2022���˾��̵����Ҫ��2020������xƽ���ף�
���˾��̵�ÿ����1ƽ���ף��˾�����ˮ������![]() ƽ���ף��˿�Ҳ����֮����5��
ƽ���ף��˿�Ҳ����֮����5��
��2022���˿�����5x���˾�����ˮ������![]() xƽ���ף�
xƽ���ף�
��2020�������������˿�����Ϊ300���ˣ�����ˮ�����Ϊ�˾�4ƽ���ף�
��2020������ˮ�����Ϊ300��4=1200��ƽ���ף���
��2020���̵����Ϊ2500+3500=6000��ƽ���ף���
��2020���˾��̵����Ϊ��6000��300=20��ƽ���ף���
��2022����̵������������ˮ�������Ҫ��2020��Ļ���������75%��
�ࣨ300+5x��(20+x)+(300+5x)(0.2x+4)=(6000+1200)��(1+75%)��
����ã�x2+80x-900=0��
��ã�x1=10��x2=-90(��ȥ)��
��2022���˾��̵����Ҫ��2020������10ƽ���ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ���ݽ�̨�IJ���ʾ��ͼ��֧�����߶�![]() �ͻ�
�ͻ�![]() ��
��![]() Ϊ̨�棬
Ϊ̨�棬![]() ��ˮƽ�����ϣ�
��ˮƽ�����ϣ�![]() ���߶�
���߶�![]() ��
��![]() ��
��![]() ��
��
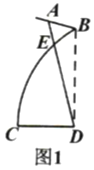
��1����̨���ϵ�![]() ���ĸ߶ȣ������ȷ��
���ĸ߶ȣ������ȷ��![]() ����
����
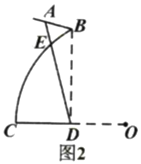
��2����ͼ2������![]() ����Բ��Բ��Ϊ��
����Բ��Բ��Ϊ��![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ����֧��
����֧��![]() �ij��ȣ������ȷ��
�ij��ȣ������ȷ��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����69��ѧΪ����֯һ������Կ������ڱ�У�����ȡ��������ѧ����������ÿ����ϲ����һ�������˶�������ͳ�ƣ�����������������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ��
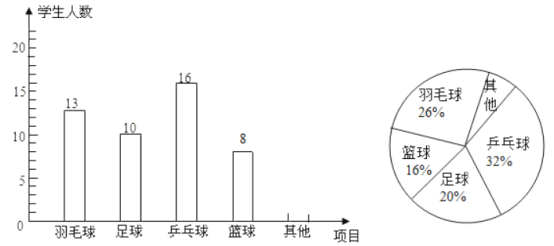
�������������Ϣ�ش��������⣺
��1���α������ѧ��������
��2��ͨ�����㲹ȫ����ͳ��ͼ��
��3����ȫУ��4500��ѧ����������Ƹ�У��ϲ�������˶���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ǿѧ�������������ʶ����Ӧ��ͣ�β�ͣѧ�����٣�ijУ��֯��һ�Ρ��������֪ʶ��ר������ѧϰ����������һ��ȫУ2500��ѧ�����μӵ����ϲ��ԣ��ľ����������ȡ��100�ݴ�����з���ͳ�ƣ����ֿ��Գɼ���![]() �֣�����ͷ�Ϊ51�֣���߷�Ϊ����100�֣������������²�������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺
�֣�����ͷ�Ϊ51�֣���߷�Ϊ����100�֣������������²�������ͳ��ͼ���������ͼ���ṩ����Ϣ������������⣺
�����Σ��֣� | Ƶ�����ˣ� | Ƶ�� |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
�ϼ� | 100 | 1 |

��1����գ�![]() ________��
________��![]() ________��
________��![]() ________��
________��
��2����Ƶ���ֲ�ֱ��ͼ����������
��3����У�Գɼ�Ϊ![]() ��ѧ�����н��������ɼ��Ӹ߷ֵ��ͷ���һ���������Ƚ�������һ���������Ƚ�����������Ϊ
��ѧ�����н��������ɼ��Ӹ߷ֵ��ͷ���һ���������Ƚ�������һ���������Ƚ�����������Ϊ![]() ���������ȫУ��ö��Ƚ���ѧ��������
���������ȫУ��ö��Ƚ���ѧ��������
��4����ϵ���������Ϊ��������������ʶ�������ѧУ��һ�������Խ��飮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ�
���õ�![]() �����е�
�����е�![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ����
����![]() ����ת�����У���
����ת�����У���![]() ����
����![]() �ij�Ϊ_________��
�ij�Ϊ_________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�п�չ�Ļ������Ż�У�����С��Ҫ��һ�鿿ǽ��ǽ��![]() ���Ŀյ�����һ�����λ�
���Ŀյ�����һ�����λ�![]() ������һ�߿�ǽ�����������ܳ�Ϊ
������һ�߿�ǽ�����������ܳ�Ϊ![]() ��դ��Χ�ɣ����軨��ǽ��һ�߳�Ϊ
��դ��Χ�ɣ����軨��ǽ��һ�߳�Ϊ![]() ���������Ϊ
���������Ϊ![]() ��
��
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�����������Ļ�����ܴﵽ![]() �����ܣ������ʱ
�����ܣ������ʱ![]() ��ֵ�������ܣ���˵�����ɣ�
��ֵ�������ܣ���˵�����ɣ�
��3�����ݣ�1������õĺ�����ϵʽ���жϵ�![]() ȡ��ֵʱ�������������������Ƕ��٣�
ȡ��ֵʱ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������2![]() ��3
��3![]() ��5
��5![]() +(��3
+(��3![]() )
)
��2��ijͬѧ��һ����ѧ�⣺����������ʽA��B��B=3x2��2x��6������A+B������λͬѧ�ѡ�A+B�����ɡ�A��B�������������ǩ�8x2+7x+10����ôA+B����ȷ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У�����ij��P��P����ԭ�㣩�����Ե�PΪԲ�ģ�![]() ��Ϊ�뾶ԲΪ��P�İ볤Բ�����ڵ�Q��������P�İ볤Բ
��Ϊ�뾶ԲΪ��P�İ볤Բ�����ڵ�Q��������P�İ볤Բ![]() ��ԭ����ת���ܹ�ʹ�õ�Qλ�ڵ�P�İ볤Բ�ڲ���Բ�ϣ���Ƶ�Q�ܱ���P�볤�����P�ܰ볤�����Q����
��ԭ����ת���ܹ�ʹ�õ�Qλ�ڵ�P�İ볤Բ�ڲ���Բ�ϣ���Ƶ�Q�ܱ���P�볤�����P�ܰ볤�����Q����
��1����ƽ��ֱ������ϵxoy�У���M��2��0�������M�İ볤Բ�����Ϊ �����и���![]() ���ܱ���M�볤����ĵ��� ��
���ܱ���M�볤����ĵ��� ��
��2����֪��![]() ��
��
�ٵ�N��0��n������t=1ʱ���߶�EF�ϵ����е�����Ա���N�볤������n��ȡֵ��Χ��
��������ƽ���ϵ�����㣨ԭ����⣩�����ܰ볤�����߶�EF�ϵ����е㣬ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ���![]() �У�
�У�![]() Ϊ���ߣ����߶�
Ϊ���ߣ����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ����
����![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
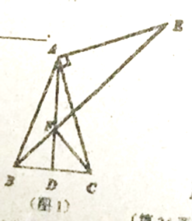
��1����![]() ����
����![]()
![]() ��
��
��2����![]() �Ƕ۽�ʱ��
�Ƕ۽�ʱ��
������ͼ2�������ⲹȫͼ�Σ��������Ӧ��ĸ��
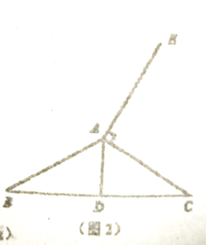
��̽��ͼ2��![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com