
【题目】图1是一个演讲台的侧面示意图,支架是线段![]() 和弧
和弧![]() ,
,![]() 为台面,
为台面,![]() 在水平地面上,
在水平地面上,![]() .线段
.线段![]() ,
,![]() ,
,![]() .
.
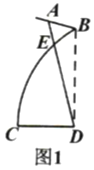
(1)求台面上点![]() 处的高度(结果精确到
处的高度(结果精确到![]() );
);
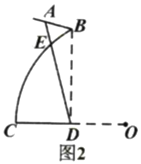
(2)如图2,若弧![]() 所在圆的圆心为点
所在圆的圆心为点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,求支架
,求支架![]() 的长度(结果精确到
的长度(结果精确到![]() ).
).
【答案】(1)100cm;(2)121cm
【解析】
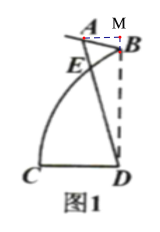
(1)过点A作CD的平行线交DB的延长线于点M,在RtAMB中,求出MB,MA的长,在RtAMD中,求出MD的长,进而即可求解;
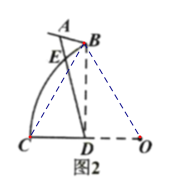
(2)连接BC,BD,易证BCO是等边三角形,∠BOC=60°,从而求出OB的长,进而利用弧长公式,即可求解.
(1)过点A作CD的平行线交DB的延长线于点M,
∵![]() 在水平地面上,
在水平地面上,![]() .线段
.线段![]() ,
,![]() ,
,![]() ,AM∥CD,
,AM∥CD,
∴∠MAD=![]() ,∠MAB=∠MAD-∠DAB=75°-60°=15°,
,∠MAB=∠MAD-∠DAB=75°-60°=15°,
∴在RtAMB中,MB=ABsin15°,MA=ABcos15°,在RtAMD中,MD=MAtan75°=
ABcos15°tan75°,
∴BD=MD-MB= ABcos15°tan75°- ABsin15°≈108.1-7.8≈100cm,
∴台面上点![]() 处的高度是100cm;
处的高度是100cm;
(2)连接BC,BD,
∵![]() ,
,![]() ,即:BD垂直平分CD,
,即:BD垂直平分CD,
∴BO=BC,
∵点![]() 为弧
为弧![]() 所在圆的圆心,
所在圆的圆心,
∴BO=CO,
∴BCO是等边三角形,即∠BOC=60°,
∵BD≈100cm,
∴OB=BD÷sin60°=100÷![]() ≈115.5cm,
≈115.5cm,
∴弧![]() 的长=
的长=![]() ≈121cm.
≈121cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告.已知当这种商品每月的广告费用为m(千元)时,每月销售量将是原销售量的p倍,且p =![]() .
.
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,顶点O(0,0),A(﹣2,3),B(2,3),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第2020次旋转结束时,点D的坐标为( )
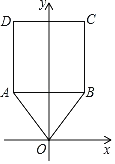
A.(﹣2,7)B.(7,2)C.(2,﹣7)D.(﹣7,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
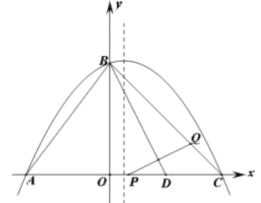
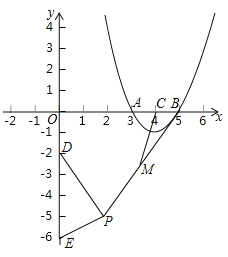
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的顶点坐标;
求这条抛物线的顶点坐标;
![]() 已知
已知![]() (点
(点![]() 在线段
在线段![]() 上),有一动点
上),有一动点![]() 从点
从点![]() 沿线段
沿线段![]() 以每秒
以每秒![]() 个单位长度的速度移动:同时另一个点
个单位长度的速度移动:同时另一个点![]() 以某一速度从点
以某一速度从点![]() 沿线段
沿线段![]() 移动,经过
移动,经过![]() 的移动,线段
的移动,线段![]() 被
被![]() 垂直平分,求
垂直平分,求![]() 的值;
的值;
![]() 在
在![]() 的情况下,抛物线的对称轴上是否存在一点
的情况下,抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的值最小?若存在,请求出点
的值最小?若存在,请求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,将边长为4的菱形![]() 的边
的边![]() 固定在
固定在![]() 轴上,开始时
轴上,开始时![]() ,现把菱形向左推,使点
,现把菱形向左推,使点![]() 落在
落在![]() 轴正半轴上的点
轴正半轴上的点![]() 处,则下列说法中错误的是( )
处,则下列说法中错误的是( )
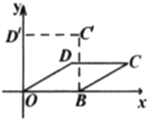
A.点![]() 的坐标为
的坐标为![]() B.
B.![]()
C.点![]() 移动的路径长度为4个单位长度D.
移动的路径长度为4个单位长度D.![]() 垂直平分
垂直平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线相等的四边形一定是矩形
B.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
C.如果有一组数据为5,3,6,4,2,那么它的中位数是6
D.“用长分别为![]() 、12cm、
、12cm、![]() 的三条线段可以围成三角形”这一事件是不可能事件
的三条线段可以围成三角形”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象经过点
)的图象经过点![]() 和
和![]() ,直线
,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
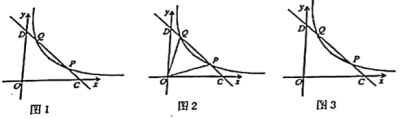
(1)求![]() 的度数;
的度数;
(2)如图2,连接![]() 、
、![]() ,当
,当![]() 时,求此时
时,求此时![]() 的值:
的值:
(3)如图3,点![]() ,点
,点![]() 分别在
分别在![]() 轴和
轴和![]() 轴正半轴上的动点.再以
轴正半轴上的动点.再以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .若点
.若点![]() 恰好在函数
恰好在函数![]() (
(![]() 为常数,
为常数,![]() ,
,![]() )的图象上,且四边形
)的图象上,且四边形![]() 为平行四边形,求此时
为平行四边形,求此时![]() 、
、![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为国家级开发区的两江新区,大小公园星罗棋布,称为“百园之城”.该区2018年绿地总面积为2500万平方米,2020年绿地总面积将比2018年增加3500万平方米,人口比2018年增加50万人.这样,2020年该区人均绿地面积是2018年人均绿地面积的2倍.
(1)求2020年两江新区的人口数量;
(2)2020年起,为了更好地建设“一半山水一半城”的美丽新区,吸引外来人才落户两江新区,新区管委会在增加绿地面积的同时大力扩展配套水域面积.根据调查,2020年新区的配套水域面积为人均4平方米.在2020年的基础上,如果人均绿地每增加1平方米,人均配套水域将增加![]() 平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com