
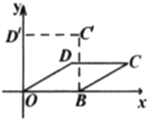
【题目】我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,将边长为4的菱形![]() 的边
的边![]() 固定在
固定在![]() 轴上,开始时
轴上,开始时![]() ,现把菱形向左推,使点
,现把菱形向左推,使点![]() 落在
落在![]() 轴正半轴上的点
轴正半轴上的点![]() 处,则下列说法中错误的是( )
处,则下列说法中错误的是( )
A.点![]() 的坐标为
的坐标为![]() B.
B.![]()
C.点![]() 移动的路径长度为4个单位长度D.
移动的路径长度为4个单位长度D.![]() 垂直平分
垂直平分![]()
【答案】C
【解析】
先证明四边形OBC′D′是正方形,且边长=4,即可判断A;由平行线的性质得∠OBC的度数,进而得到![]() ,即可判断B;根据弧长公式,求出点
,即可判断B;根据弧长公式,求出点![]() 移动的路径长度,即可判断C;证明CD⊥BC′,BC′=BC=2BE,即可判断D.
移动的路径长度,即可判断C;证明CD⊥BC′,BC′=BC=2BE,即可判断D.
∵四边形OBCD是菱形,
∴OB=BC=CD=OD,
∴OB=BC′=C′D′=OD′,
∵∠BOD′=90°,
∴四边形OBC′D′是正方形,且边长=4,
∴点![]() 的坐标为
的坐标为![]() ,故A不符合题意.
,故A不符合题意.
∵![]() ,OD∥BC,
,OD∥BC,
∴∠OBC=180°-30°=150°,
∵∠OBC′=90°,
∴![]() ,故B不符合题意.
,故B不符合题意.
∵点![]() 移动的路径是以OD长为半径,圆心角为∠DOD′=90°-30°=60°的弧长,
移动的路径是以OD长为半径,圆心角为∠DOD′=90°-30°=60°的弧长,
∴点![]() 移动的路径长度=
移动的路径长度=![]() =
=![]() ,故C符合题意.
,故C符合题意.
设CD与BC′交于点E,
∵在菱形OBCD中,∠C=![]() ,
,
∵![]() ,
,
∴∠BEC=180°-60°-30°=90°,即CD⊥BC′,
∴BC′=BC=2BE,
∴![]() 垂直平分
垂直平分![]() ,故D不符合题意.
,故D不符合题意.
故先C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
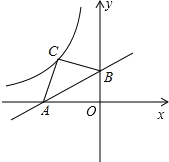
【题目】直线y=![]() x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=
x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=![]() (x<0)的图象过点C,则m=_____.
(x<0)的图象过点C,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最小值为( )
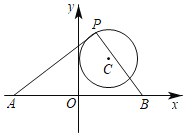
A.4B.3C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
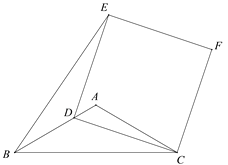
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住武汉园博园元宵灯会的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1) 求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过765元,那么该商店共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个演讲台的侧面示意图,支架是线段![]() 和弧
和弧![]() ,
,![]() 为台面,
为台面,![]() 在水平地面上,
在水平地面上,![]() .线段
.线段![]() ,
,![]() ,
,![]() .
.
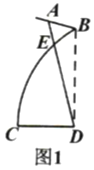
(1)求台面上点![]() 处的高度(结果精确到
处的高度(结果精确到![]() );
);
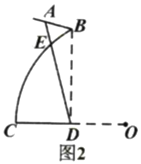
(2)如图2,若弧![]() 所在圆的圆心为点
所在圆的圆心为点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,求支架
,求支架![]() 的长度(结果精确到
的长度(结果精确到![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
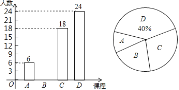
【题目】为深化课程改革,提高学生的综合素质,我校开设了形式多样的校本课程.为了解校本课程在学生中最受欢迎的程度,学校随机抽取了部分学生进行调查,从A:天文地理;B:科学探究;C:文史天地;D:趣味数学;四门课程中选你喜欢的课程(被调查者限选一项),并将调查结果绘制成两个不完整的统计图,如图所示,根据以上信息,解答下列问题:
(1)本次调查的总人数为 人,扇形统计图中A部分的圆心角是 度;
(2)请补全条形统计图;
(3)根据本次调查,该校400名学生中,估计最喜欢“科学探究”的学生人数为多少?
(4)为激发学生的学习热情,学校决定举办学生综合素质大赛,采取“双人同行,合作共进”小组赛形式,比赛题目从上面四个类型的校本课程中产生,并且规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,小琳和小金组成了一组,求他们抽到“天文地理”和“趣味数学”类题目的概率是多少?(请用画树状图或列表的方法求)
查看答案和解析>>
科目:初中数学 来源: 题型:
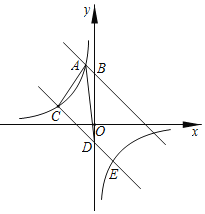
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求直线AB的解析式;
(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求![]() 的面积;
的面积;
(3)设直线CD的解析式为![]() ,根据图象直接写出不等式
,根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com