
【题目】如图1,在等腰![]() 中,
中,![]() 为中线,将线段
为中线,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ;得到线段
;得到线段![]() 连接
连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
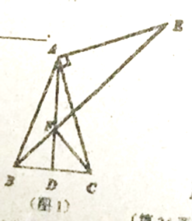
(1)若![]() ,则
,则![]()
![]() ;
;
(2)若![]() 是钝角时,
是钝角时,
①请在图2中依题意补全图形,并标出对应字母;
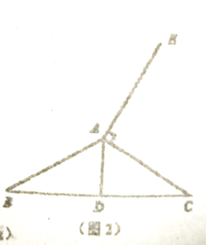
②探究图2中![]() 的形状,并说明理由;
的形状,并说明理由;
③若![]() 则
则![]() .
.
【答案】(1)45°;(2)①见解析;②![]() 是等腰直角三角形,理由见解析;③
是等腰直角三角形,理由见解析;③![]()
【解析】
(1)根据等腰△ABC的性质可得∠BAD的角度,从而得出∠ABD的角度;在等腰△ABE中,可推导得出∠ABE的大小,从而得出∠FBC;
(2)①根据题干要求补全图形即可;
②如下图,根据等腰△FBC的性质可得到△FAB≌△FAC,从而得∠FBA=∠FCA,再根据旋转特点,可得∠FBA=∠AFB,最后利用Rt△AEC和△CEF之间的角度转化可得∠EFC=90°,从而得出三角形形状;
③在Rt△AEC中,可求得EC的长,再在Rt△BFC中求得FC的长,最后在Rt△EFC中得出EF的长.
(1)∵AE是AC绕点A逆时针旋转90°所得
∴∠CAE=90°,CA=AE
∵AB=AC,
∴AB=AE
∵∠BAC=30°,AD是等腰三角形的中线
∴∠BAD=∠DAC=15°,AD⊥BC
∴∠BAE=120°
∴在△ABE中,∠ABE=∠E=30°
在△ADB中,∠ABD=75°
∴∠FBC=45°
(2)①如下图:
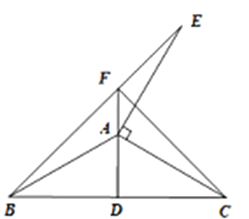
![]() 是等腰直角三角形
是等腰直角三角形
②![]() 是等腰直角三角形,理由如下
是等腰直角三角形,理由如下
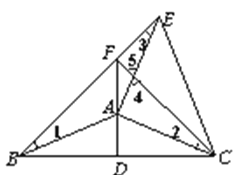
![]()
![]() .
.
![]() 是
是![]() 的垂直平分线
的垂直平分线
![]()
又![]()
![]()
![]()
由旋转可知![]() ,又
,又![]() .
.
![]()
![]()
![]()
又![]()
![]()
即
又![]() .
.
![]() 为等腰直角三角形
为等腰直角三角形
③∵AB=5,
∴AC=5
∵△ACE是等腰直角三角形
∴可得:AE=5,EC=![]()
∵BC=8
∴在等腰直角三角形FBC中,FB=FC=4![]()
∴在Rt△EFC中,EF=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】作为国家级开发区的两江新区,大小公园星罗棋布,称为“百园之城”.该区2018年绿地总面积为2500万平方米,2020年绿地总面积将比2018年增加3500万平方米,人口比2018年增加50万人.这样,2020年该区人均绿地面积是2018年人均绿地面积的2倍.
(1)求2020年两江新区的人口数量;
(2)2020年起,为了更好地建设“一半山水一半城”的美丽新区,吸引外来人才落户两江新区,新区管委会在增加绿地面积的同时大力扩展配套水域面积.根据调查,2020年新区的配套水域面积为人均4平方米.在2020年的基础上,如果人均绿地每增加1平方米,人均配套水域将增加![]() 平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
A.1B.1.5C.4-![]() D.4-
D.4-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
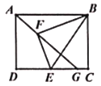
【题目】图①、图②都是![]() 的正方形网格,每个小正方形的顶点叫做格点.
的正方形网格,每个小正方形的顶点叫做格点.![]() 的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)在图①中过点![]() 作
作![]() 面积两等分的射线.
面积两等分的射线.
(2)在图②中过点![]() 作所有将
作所有将![]() 面积分成1:2的两部分的射线.
面积分成1:2的两部分的射线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,它的两边分别交边
旋转,它的两边分别交边![]() 、
、![]() (或它们的延长线)于点
(或它们的延长线)于点![]() 、
、![]() .
.
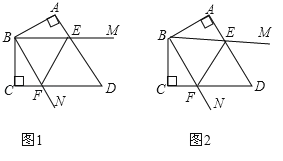
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),
时(如图1),
①求证:![]() ;
;
②求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到如图2所示的位置时,
旋转到如图2所示的位置时,![]() ,此时,(1)中的两个结论是否还成立?请直接回答.
,此时,(1)中的两个结论是否还成立?请直接回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com