
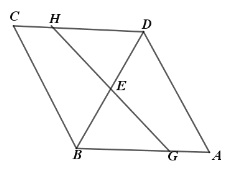
【题目】如图,菱形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 的中点.点
的中点.点![]() 是
是![]() 边上一动点,
边上一动点,![]() 延长线交
延长线交![]() 于点
于点![]() 则
则![]() 长度可能为( )
长度可能为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
当GH⊥AB时,GH的长度最短;当GH与AC重合时,GH的长度最长,故可得出GH的取值范围,从而判定选项.
如下图,当GH⊥AB时,GH的长度最短,过点C作AB的垂线交AB延长线于点F
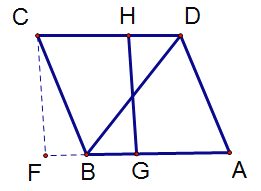
∵四边形ABCD是菱形,
∴FG∥CH
∵GH⊥AB,CF⊥AB,
![]() HG
HG![]() CF
CF
∴四边形GHCF是矩形
∵菱形ABCD中,∠A=60°,边长为2
∴CB=2,∠CBF=60°
∴在Rt △CBF中,FB=1,CF=![]()
∴HG=![]()
如下图,当GH与AC重合时,GH的长度最长,过点C作AB的垂线交AB延长线于点F

∵∠BAD=60°,菱形ABCD的边长为2
∴∠BAC=∠BCA=30°,CB=2
∴∠CBF=60°
∴在Rt△CBF中,BF=1
∴FA=3
∴在Rt△CAF中,CF=![]() ,AC=2
,AC=2![]()
∴![]() ≤GH≤2
≤GH≤2![]()
故选:B


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
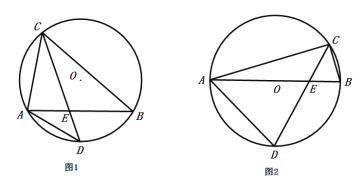
(1)求证:△ADE∽△CDA
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :家庭汽车,
:家庭汽车,![]() :公交车,
:公交车,![]() :电动车,
:电动车,![]() :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
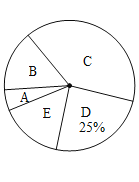

(1)本次调查中,一共调查了 名市民;扇形统计图中,![]() 项对应的扇形圆心角是_____
项对应的扇形圆心角是_____ ![]() ;
;
(2)补全条形统计图;
(3)若甲上班时从![]() 三种交通工具中随机选择一种, 乙上班时从
三种交通工具中随机选择一种, 乙上班时从![]() 三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选
三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选![]() 种交通工具上班的概率.
种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国70周年,某校举办了爱我中华知识竞赛活动.该校南、北两个校区七年级各有300名学生参加竞赛活动.为了解这两个校区参赛学生成绩情况,从中各随机抽取了10名学生的成绩进行调查,过程如下:
(收集、整理、描述数据)根据随机抽取的10名学生的成绩,制作了如下统计图表:
(说明:成绩90分及以上为优秀,80-89分为良好,60-79分为合格,60分以下为不合格)
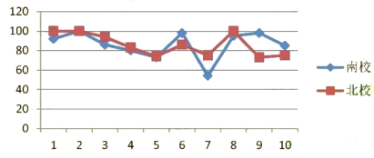
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
(分析数据)对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数如下表:
校区 | 平均数(分) | 中位数(分) | 众数(分) |
南校 | 87 | 90.5 | |
北校 | 86 | 100 |
(得出结论)综合上述统计全过程,回答下列问题:
(1)补全表格.
(2)估计北校七年级学生竞赛成绩为优秀的人数.
(3)你认为哪个校区的七年级学生竞赛成绩比较好?说明你的理由.(从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
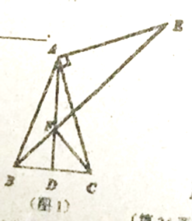
【题目】如图1,在等腰![]() 中,
中,![]() 为中线,将线段
为中线,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ;得到线段
;得到线段![]() 连接
连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]()
![]() ;
;
(2)若![]() 是钝角时,
是钝角时,
①请在图2中依题意补全图形,并标出对应字母;
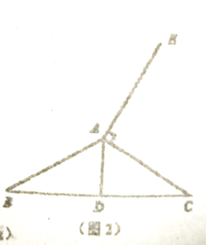
②探究图2中![]() 的形状,并说明理由;
的形状,并说明理由;
③若![]() 则
则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
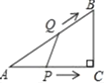
A.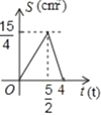 B.
B.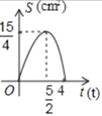 C.
C. D.
D.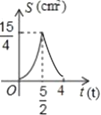
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:
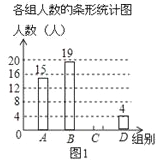
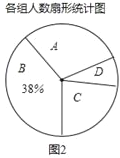
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
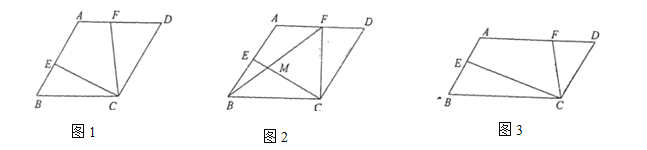
(2)如图2,若![]() ,且点
,且点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() ;
;
(3)如图3,若![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 三之间的数量关系,说明理由.
三之间的数量关系,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com