
【题目】在平行四边形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
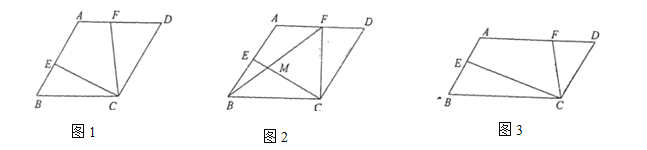
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,且点
,且点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() ;
;
(3)如图3,若![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 三之间的数量关系,说明理由.
三之间的数量关系,说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接AC,根据题意判定平行四边形ABCD为菱形,△ABC为等边三角形,然后利用AAS定理判定△BCE≌△ACF,从而得出BE=AF,使问题得解;
(2)连接AC,过点M作MN⊥CF,由含30°直角三角形的性质求得![]() ,
,![]() ,设CN=x,则
,设CN=x,则![]() ,然后利用平行判定△FMN∽△FBC,根据相似三角形的性质求得
,然后利用平行判定△FMN∽△FBC,根据相似三角形的性质求得![]() ,然后利用勾股定理求解即可;
,然后利用勾股定理求解即可;
(3)连接AC,过点A作AK⊥BC,在DA上截取DH=CD,根据有一个角是60°的等腰三角形是等边三角形判定△HCD是等边三角形,然后根据AA定理判定△BCE ∽△FCH,根据相似三角形的性质求得![]() ,即HF=kBE,从而使问题得解.
,即HF=kBE,从而使问题得解.
解:(1)连接AC
因为在平行四边形ABCD中,![]() ,
,![]()
∴平行四边形ABCD为菱形,△ABC为等边三角形
∴AC=BC,∠B=∠BAC=∠DAC=∠ACB=60°,
又∵![]()
∴∠ACE+∠BCE=∠ACE+∠ACF
∴∠BCE=∠ACF
∴△BCE≌△ACF
∴BE=AF
∴AB=AE+BE=![]()
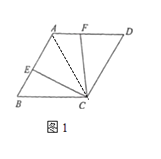
(2)连接AC,过点M作MN⊥CF
由(1)已证,△ABC为等边三角形,△BCE≌△ACF
∵![]() 为
为![]() 的中点
的中点
∴CE⊥AB
∴在Rt△BCE中,∠BCE=30°
∴![]() ,
,![]()
由题意![]() ,∴∠BCF=90°
,∴∠BCF=90°
在Rt△AMCN中,∠CMN=30°
设CN=x,则![]()
∵MN⊥CF
∴MN∥BC
∴△FMN∽△FBC
∴![]() ,
,![]()
解得:![]()
∴![]()
在Rt△FMN中,![]()
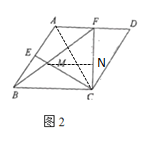
(3)由题意可知,在平行四边形ABCD中,∠B=∠D=60°,![]()
连接AC,过点A作AK⊥BC,在DA上截取DH=CD
∵DH=CD,∠B=∠D=60°
∴△HCD是等边三角形
∴∠HCD=60°
又∵∠ECF=60°
∴∠BCE+∠ECH=∠FCH+∠ECH
∴∠BCE =∠FCH
∴△BCE ∽△FCH
∴![]() ,即HF=kBE
,即HF=kBE
∴CD=DF+HF=DF+ kBE
又∵![]()
∴![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
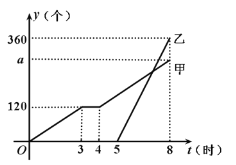
【题目】某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两车间各自加工零件的数量y(个)与甲车间加工时间t(时)之间的函数图象如图所示.
(1)求乙车间加工零件的数量y与甲车间加工时间t之间的函数关系式,并写出t的取值范围.
(2)求甲车间加工零件总量a.
(3)当甲、乙两车间加工零件总数量为320个时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(用虚线表示画图过程,实线表示画图结果)
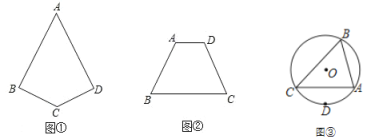
(1)如图①,四边形 ABCD 中,AB=AD,∠B=∠D,画出四边形 ABCD 的对称轴 m;
(2)如图②,四边形 ABCD 中,AD∥BC,∠A=∠D,画出 BC 边的垂直平分线 n.
(3)如图③,△ABC 的外接圆的圆心是点 O,D 是![]() 的中点,画一条直线把△ABC 分成面积相等的两部分.
的中点,画一条直线把△ABC 分成面积相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设![]() ,求y关于
,求y关于![]() 的函数解析式及定义域;
的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果![]() 与
与![]() 相似,求线段BP的长.
相似,求线段BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的图象经过坐标原点
的图象经过坐标原点![]() ,且与
,且与![]() 轴另交点为
轴另交点为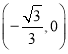 .
.
(1)求抛物线![]() 的解析式;
的解析式;
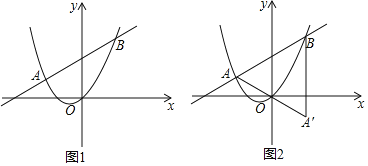
(2)如图![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() (点
(点![]() 在第二象限),求
在第二象限),求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)在(2)中,若![]() ,设点
,设点![]() 是点
是点![]() 关于原点
关于原点![]() 的对称点,如图
的对称点,如图![]() .平面内是否存在点
.平面内是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,分别过点![]() ,
,![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 和
和![]() ,探究直线
,探究直线![]() 、
、![]() 与函数
与函数![]() 的图象(双曲线)之间的关系,下列结论正确的是( )
的图象(双曲线)之间的关系,下列结论正确的是( )
A.两条直线可能都不与双曲线相交
B.当![]() 时,两条直线与双曲线的交点到原点的距离不相等
时,两条直线与双曲线的交点到原点的距离不相等
C.当![]() 时,两条直线与双曲线的交点都在
时,两条直线与双曲线的交点都在![]() 轴左侧
轴左侧
D.当![]() 时,两条直线与双曲线的交点都在
时,两条直线与双曲线的交点都在![]() 轴右侧
轴右侧
查看答案和解析>>
科目:初中数学 来源: 题型:
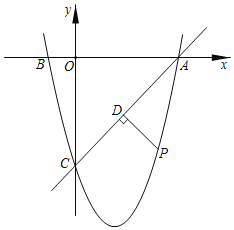
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com