
【题目】抛物线![]() 的图象经过坐标原点
的图象经过坐标原点![]() ,且与
,且与![]() 轴另交点为
轴另交点为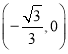 .
.
(1)求抛物线![]() 的解析式;
的解析式;
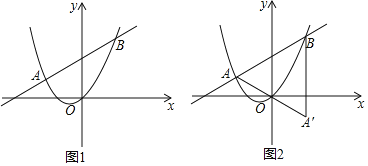
(2)如图![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() (点
(点![]() 在第二象限),求
在第二象限),求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)在(2)中,若![]() ,设点
,设点![]() 是点
是点![]() 关于原点
关于原点![]() 的对称点,如图
的对称点,如图![]() .平面内是否存在点
.平面内是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)y=x2+![]() x;(2)y2﹣y1==
x;(2)y2﹣y1==![]() (m>0);(3)存在符合题意的点P,且以点A、B、A′、P为顶点的菱形分三种情况,点P的坐标为(2
(m>0);(3)存在符合题意的点P,且以点A、B、A′、P为顶点的菱形分三种情况,点P的坐标为(2![]() ,
,![]() )、(﹣
)、(﹣![]() ,
,![]() )和(﹣
)和(﹣![]() ,﹣2).
,﹣2).
【解析】
(1)根据点的坐标,利用待定系数法即可求出抛物线F的解析式;
(2)将直线l的解析式代入抛物线F的解析式中,可求出x1、x2的值,利用一次函数图象上点的坐标特征可求出y1、y2的值,做差后即可得出y2-y1的值;
(3)根据m的值可得出点A、B的坐标,利用对称性求出点A′的坐标.利用两点间的距离公式(勾股定理)可求出AB、AA′、A′B的值,由三者相等即可得出△AA′B为等边三角形;结合菱形的性质,可得出存在符合题意得点P,设点P的坐标为(x,y),分三种情况考虑:(i)当A′B为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;(ii)当AB为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;(iii)当AA′为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标.综上即可得出结论.
(1)∵抛物线y=x2+bx+c的图象经过点(0,0)和(-![]() ,0),
,0),
∴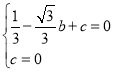 ,
,
解得: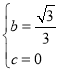 ,
,
∴抛物线F的解析式为y=x2+![]() x.
x.
(2)将y=![]() x+m代入y=x2+
x+m代入y=x2+![]() x,得:x2=m,
x,得:x2=m,
解得:x1=﹣![]() ,x2=
,x2=![]() ,
,
∴y1=﹣![]() +m,y2=
+m,y2=![]() +m,
+m,
∴y2﹣y1=(![]() +m)﹣(﹣
+m)﹣(﹣![]() +m)=
+m)=![]() (m>0).
(m>0).
(3)∵m=![]() ,
,
∴点A的坐标为(﹣![]() ,
,![]() ),点B的坐标为(
),点B的坐标为(![]() ,2).
,2).
∵点A′是点A关于原点O的对称点,
∴点A′的坐标为(![]() ,﹣
,﹣![]() ).
).
由两点距离公式可得:AA′=AB=A′B=![]() ,
,
∴存在符合题意的点P,且以点A、B、A′、P为顶点的菱形分三种情况,设点P的坐标为(x,y).
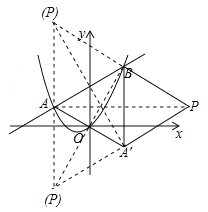
(i)当A′B为对角线时,有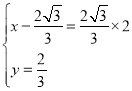 ,
,
解得: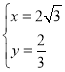 ,
,
∴点P的坐标为(2![]() ,
,![]() );
);
(ii)当AB为对角线时,有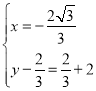 ,
,
解得: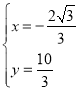 ,
,
∴点P的坐标为(﹣![]() ,
,![]() );
);
(iii)当AA′为对角线时,有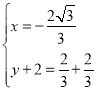 ,
,
解得: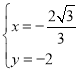 ,
,
∴点P的坐标为(﹣![]() ,﹣2).
,﹣2).



科目:初中数学 来源: 题型:
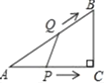
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
A.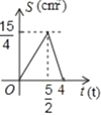 B.
B.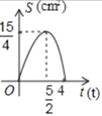 C.
C. D.
D.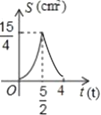
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
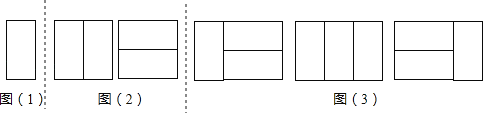
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
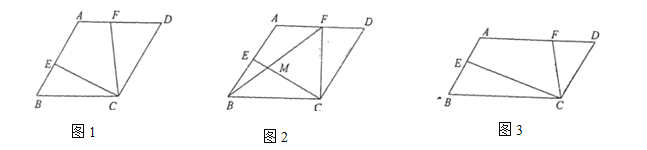
(2)如图2,若![]() ,且点
,且点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() ;
;
(3)如图3,若![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 三之间的数量关系,说明理由.
三之间的数量关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
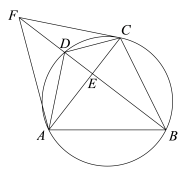
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,顶点为
之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]()
③将该抛物线向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得抛物线解析式为
个单位,所得抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() 点
点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中正确判断的序号是( )
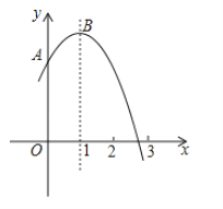
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一枚均匀的正四面体,四个面上分别标有数字1,2,3,4,小红随机地抛掷一次,把着地一面的数字记为x;另有三张背面完全相同,正面上分别写有数字-2,-1,1的卡片,小亮将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后他们计算出S=x+y的值.
(1)用树状图或列表法表示出S的所有可能情况;
(2)分别求出当S=0和S<2时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com