
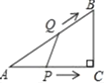
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
A. B.
B. C.
C. D.
D.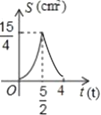
【答案】C
【解析】
分两段讨论:当0≤t≤![]() 时,过Q作QD⊥AC交AC于点D,S△APQ=
时,过Q作QD⊥AC交AC于点D,S△APQ=![]() ×AP×QD;当
×AP×QD;当![]() <t≤4时,S△APQ=S△ABC-S△CPQ-S△ABQ.
<t≤4时,S△APQ=S△ABC-S△CPQ-S△ABQ.
解:由题可知,![]() s时点Q运动到点B,
s时点Q运动到点B,
①当0≤t≤![]() 时,点Q在AB上,
时,点Q在AB上,
∴AQ=2t,AP=t,
过Q作QD⊥AC交AC于点D,
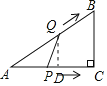
∵Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,
∴BC=3cm,
∴![]() ,,
,,
∴QD=![]() ,
,
S△APQ=![]() ×AP×QD=
×AP×QD=![]() ×t×
×t×![]() =
=![]() ,
,
②当![]() <t≤4时,点Q在BC上,如图,
<t≤4时,点Q在BC上,如图,
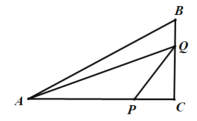
S△APQ=S△ABC-S△CPQ-S△ABQ=![]() ×3×4-
×3×4-![]() ×(4-t)×(8-2t)-
×(4-t)×(8-2t)-![]() ×4×(2t-5)=-t2+4t=-(t-2)2,
×4×(2t-5)=-t2+4t=-(t-2)2,
根据解析式可知图象是D.
故选:D.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:
(1)求点D的坐标;
(2)若反比例函数y=![]() (k≠0)的图象经过点H,则k= ;
(k≠0)的图象经过点H,则k= ;
(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且HG=![]() BC,S△ABC =12,则图中阴影部分的面积为( )
BC,S△ABC =12,则图中阴影部分的面积为( )
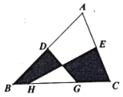
A.6B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 与函数
与函数![]() 定义新函数
定义新函数![]()
(1)若![]() 则新函数
则新函数![]() ;
;
(2)若新函数![]() 的解析式为
的解析式为![]() 则
则![]() ,
,![]() ;
;
(3)设新函数![]() 顶点为
顶点为![]() .
.
①当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值;
有最大值,并求出最大值;
②求![]() 与
与![]() 的函数解析式;
的函数解析式;
(4)请你探究:函数![]() 与新函数
与新函数![]() 分别经过定点
分别经过定点![]() ,函数
,函数![]() 的顶点为
的顶点为![]() ,新函数
,新函数![]() 上存在一点
上存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形为平行四边形时,直接写出
为顶点的四边形为平行四边形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OBC的边BC∥x轴,过点C的双曲线y=![]() (k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
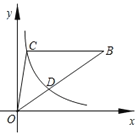
查看答案和解析>>
科目:初中数学 来源: 题型:
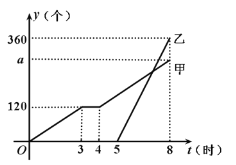
【题目】某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两车间各自加工零件的数量y(个)与甲车间加工时间t(时)之间的函数图象如图所示.
(1)求乙车间加工零件的数量y与甲车间加工时间t之间的函数关系式,并写出t的取值范围.
(2)求甲车间加工零件总量a.
(3)当甲、乙两车间加工零件总数量为320个时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的图象经过坐标原点
的图象经过坐标原点![]() ,且与
,且与![]() 轴另交点为
轴另交点为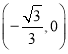 .
.
(1)求抛物线![]() 的解析式;
的解析式;
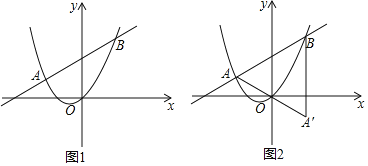
(2)如图![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() (点
(点![]() 在第二象限),求
在第二象限),求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)在(2)中,若![]() ,设点
,设点![]() 是点
是点![]() 关于原点
关于原点![]() 的对称点,如图
的对称点,如图![]() .平面内是否存在点
.平面内是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com