
【题目】如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且HG=![]() BC,S△ABC =12,则图中阴影部分的面积为( )
BC,S△ABC =12,则图中阴影部分的面积为( )
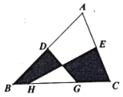
A.6B.4C.3D.2
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
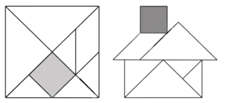
【题目】“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图①是由边长![]() 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______
的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______![]() (结果保留根号).
(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .
.

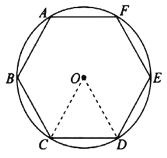
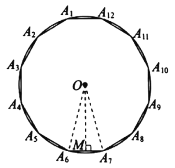
刘徽从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割的越细,圆的内接正多边形就越接近圆.设圆的半径为R,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;请写出圆内接正二十四边形的周长
;请写出圆内接正二十四边形的周长![]() ________,计算
________,计算![]() ________.(参考数据:
________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
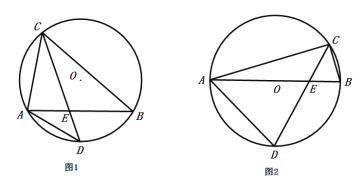
(1)求证:△ADE∽△CDA
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
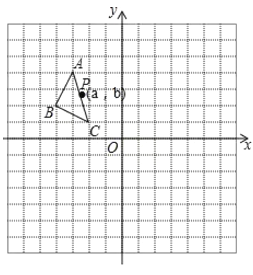
【题目】如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)将△ABC向下平移5个单位再向右平移1个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)P(a,b)是△ABC的边AC上一点,请直接写出经过两次变换后在△A2B2C2中对应的点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :家庭汽车,
:家庭汽车,![]() :公交车,
:公交车,![]() :电动车,
:电动车,![]() :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
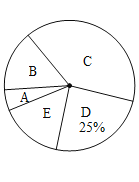

(1)本次调查中,一共调查了 名市民;扇形统计图中,![]() 项对应的扇形圆心角是_____
项对应的扇形圆心角是_____ ![]() ;
;
(2)补全条形统计图;
(3)若甲上班时从![]() 三种交通工具中随机选择一种, 乙上班时从
三种交通工具中随机选择一种, 乙上班时从![]() 三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选
三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选![]() 种交通工具上班的概率.
种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国70周年,某校举办了爱我中华知识竞赛活动.该校南、北两个校区七年级各有300名学生参加竞赛活动.为了解这两个校区参赛学生成绩情况,从中各随机抽取了10名学生的成绩进行调查,过程如下:
(收集、整理、描述数据)根据随机抽取的10名学生的成绩,制作了如下统计图表:
(说明:成绩90分及以上为优秀,80-89分为良好,60-79分为合格,60分以下为不合格)
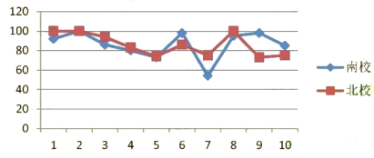
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
(分析数据)对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数如下表:
校区 | 平均数(分) | 中位数(分) | 众数(分) |
南校 | 87 | 90.5 | |
北校 | 86 | 100 |
(得出结论)综合上述统计全过程,回答下列问题:
(1)补全表格.
(2)估计北校七年级学生竞赛成绩为优秀的人数.
(3)你认为哪个校区的七年级学生竞赛成绩比较好?说明你的理由.(从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
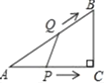
A.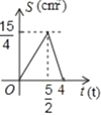 B.
B.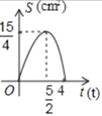 C.
C. D.
D.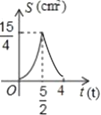
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
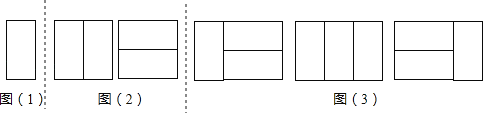
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com