
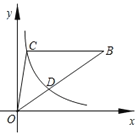
【题目】如图,△OBC的边BC∥x轴,过点C的双曲线y=![]() (k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
【答案】2
【解析】
延长BC交y轴于点E,过点D作DF⊥x轴于点FBA⊥x轴于A.由矩形与反比例函数的性质,可得S四边形ABDF=S△OBC=8,易证得△ODF∽△OBA,又由OD:DB=1:2,即可得S△ODF=![]() S四边形ABDF=
S四边形ABDF=![]() ×4=
×4=![]() ,则可求得答案.
,则可求得答案.
解:延长BC交y轴于点E,过点D作DF⊥x轴于点F,BA⊥x轴于A.
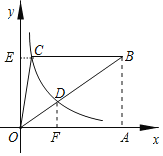
∵梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,
∴四边形OABE是矩形,
∴S△OBE=S△OAB,
∵过点C的双曲线y=![]() 交OB于点D,
交OB于点D,
∴S△OCE=S△ODF,
∴S四边形ABDF=S△OBC=8,
∵DF∥AB,
∴△ODF∽△OBA,
∵OD:DB=1:2,
∴OD:OB=1:3,
∴S△ODF:S△OAB=1:9,
∴S△ODF:S四边形ABDF=1:8,
∴S△ODF=![]() S四边形ABDF=
S四边形ABDF=![]() ×8=1,
×8=1,
∴k=2.
故答案为:2.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .
.

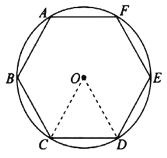
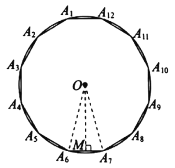
刘徽从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割的越细,圆的内接正多边形就越接近圆.设圆的半径为R,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;请写出圆内接正二十四边形的周长
;请写出圆内接正二十四边形的周长![]() ________,计算
________,计算![]() ________.(参考数据:
________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国70周年,某校举办了爱我中华知识竞赛活动.该校南、北两个校区七年级各有300名学生参加竞赛活动.为了解这两个校区参赛学生成绩情况,从中各随机抽取了10名学生的成绩进行调查,过程如下:
(收集、整理、描述数据)根据随机抽取的10名学生的成绩,制作了如下统计图表:
(说明:成绩90分及以上为优秀,80-89分为良好,60-79分为合格,60分以下为不合格)
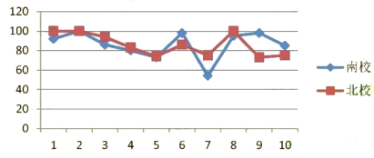
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
南校 | 92 | 100 | 86 | 80 | 73 | 98 | 54 | 95 | 98 | 85 |
北校 | 100 | 100 | 94 | 83 | 74 | 86 | 75 | 100 | 73 | 75 |
(分析数据)对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数如下表:
校区 | 平均数(分) | 中位数(分) | 众数(分) |
南校 | 87 | 90.5 | |
北校 | 86 | 100 |
(得出结论)综合上述统计全过程,回答下列问题:
(1)补全表格.
(2)估计北校七年级学生竞赛成绩为优秀的人数.
(3)你认为哪个校区的七年级学生竞赛成绩比较好?说明你的理由.(从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
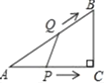
A.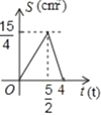 B.
B.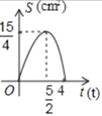 C.
C. D.
D.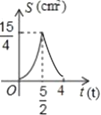
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:
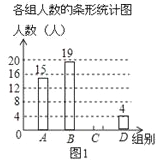
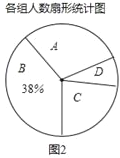
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全区范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽部分使用电瓶车的市民,就骑电瓶车戴安全帽情况(![]() :每次戴、
:每次戴、![]() :经常戴、
:经常戴、![]() :偶尔戴、
:偶尔戴、![]() :都不戴)进行问卷调查,将相关的数据制成如下统计图表.
:都不戴)进行问卷调查,将相关的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
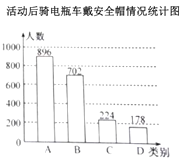
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该区约有37万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,谈谈你对交警部门宣传活动的效果的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
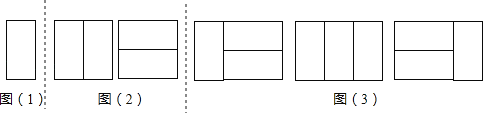
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
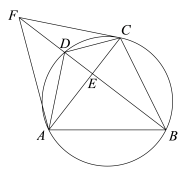
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com