
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:
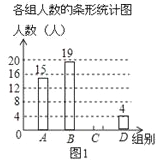
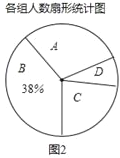
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
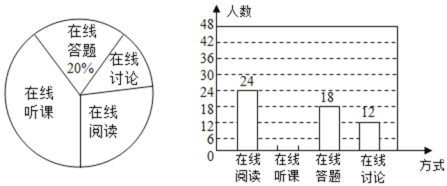
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L1:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线L2都经过y轴上的一点P,且抛物线L1与顶点Q在直线L2上,则称此直线L2与该抛物线L1具有“一带一路”关系,此时,直线L2叫做抛物线L1的“带线”,抛物线L1叫做直L2的“路线”.
(1) 若直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系,则m+n=_______.
(2) 若某“路线”L1的顶点在反比例函数![]() 的图像上,它的“带线” L2的解析式为y=2x-4,则此“路线”L的解析式为:_____________.
的图像上,它的“带线” L2的解析式为y=2x-4,则此“路线”L的解析式为:_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.

问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体![]() ,如图所示.
,如图所示.
(1)请画出这个几何体![]() 的三视图.
的三视图.
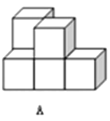
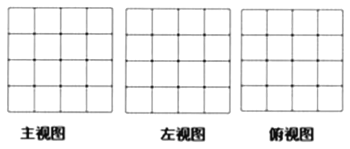
(2)若将此几何体![]() 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有 个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体![]() 上,要保持主视图和左视图不变,则最多可以添加___个小正方体.
上,要保持主视图和左视图不变,则最多可以添加___个小正方体.
(4)若另一个几何体![]() 与几何体
与几何体![]() 的主视图和左视图相同,而小正方体个数则比几何体
的主视图和左视图相同,而小正方体个数则比几何体![]() 多1个,请在图2中画出几何体
多1个,请在图2中画出几何体![]() 的俯视图中的任意两种.
的俯视图中的任意两种.
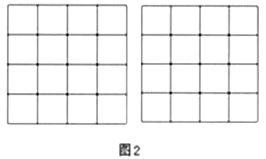
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
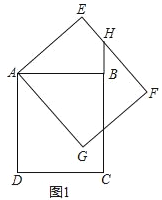
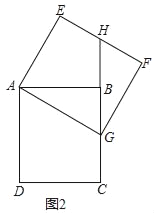
(1)求证:BH=EH;
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的月历,图中带阴影的方框恰好盖住四个数,不改变带阴影的方框的形状大小,移动方框的位置.
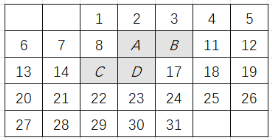
(1)若带阴影的方框盖住的4个数中,A表示的数是x,求这4个数的和(用含x的代数式表示);
(2)若带阴影的方框盖住的4个数之和为82,求出A表示的数;
(3)这4个数之和可能为38或112吗?如果可能,请求出这4个数,如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com