
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.

问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
【答案】(1)-3或1;(2)-7或1;(3)1;(4)点![]() 到4的距离;4;0;(5)点
到4的距离;4;0;(5)点![]() 到-1和到4的距离之和;5;线段CD;(6)2;2.
到-1和到4的距离之和;5;线段CD;(6)2;2.
【解析】
(1)根据数轴上两点间的距离的定义即可求解;
(2)根据数轴上两点间的距离的定义即可求解;
(3)根据数轴上两点间的距离的定义即可求解;
(4)绝对值的几何意义即可求解;
(5)绝对值的几何意义即可求解;
(6)绝对值的几何意义即可求解.
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为-3或1,
的值为-3或1,
故答案为:-3或1;
(2)![]() 即表示
即表示![]() 的点距离-3的点距离是4,则
的点距离-3的点距离是4,则![]() 的值为-7或1,
的值为-7或1,
故答案为:-7或1;
(3)![]() 即表示
即表示![]() 的点距离-4与6的距离相等,
的点距离-4与6的距离相等,
故m是-4与6的中点,
∴m=1;
故答案为:1;
(4)![]() 的几何意义是数轴上点
的几何意义是数轴上点![]() 到4的距离,当
到4的距离,当![]() 4,
4,![]() 的值最小是0
的值最小是0
故答案为:点![]() 到4的距离;4;0;
到4的距离;4;0;
(5)![]() 的几何意义是数轴上点
的几何意义是数轴上点![]() 到-1和到4的距离之和,
到-1和到4的距离之和,![]() 的最小值是5,此时点
的最小值是5,此时点![]() 在数轴上应位于线段CD上
在数轴上应位于线段CD上
故答案为:点![]() 到-1和到4的距离之和;5;线段CD;
到-1和到4的距离之和;5;线段CD;
(6)表示![]() 点
点![]() 到1,2,3的距离之和
到1,2,3的距离之和
∴![]() 的最小值是2,此时
的最小值是2,此时![]() 2.
2.
故答案为:2;2.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
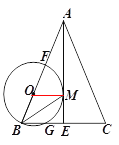
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
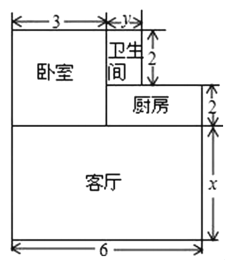
【题目】小张在贵阳购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:![]() ),解答下列问题:
),解答下列问题:
(1)用含![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)若![]() ,铺
,铺![]() 地砖的平均费用为140元,那么铺地砖的总费用为多少元?
地砖的平均费用为140元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:
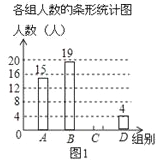
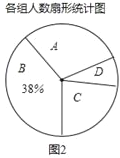
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA 交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;
(3)当![]() 时,代数式
时,代数式![]() 的值为m,求当
的值为m,求当![]() 时,求代数式
时,求代数式![]() 的值是多少?
的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com