
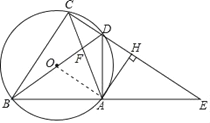
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA 交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.

【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)、连接OA,根据圆周角定理得出∠ADE=∠ADB,然后证明△DAB和△DAE全等,从而得出AB=AE,结合OB=OD得出OA∥DE,从而得出答案;(2)、根据切线的性质得出AE=AC=AB=6,根据Rt△ABD的三角函数得出答案;(3)、根据OA是中位线得出△CDF和△AOF相似,从而得出答案.
详解:(1)证明:连接OA,由圆周角定理得,∠ACB=∠ADB,∵∠ADE=∠ACB,∴∠ADE=∠ADB,
∵BD是直径,∴∠DAB=∠DAE=90°,在△DAB和△DAE中,
∠BAD=∠EAD,DA=DA,∠BDA=∠EDA,∴△DAB≌△DAE,∴AB=AE,又∵OB=OD,
∴OA∥DE,又∵AH⊥DE,∴OA⊥AH,∴AH是⊙O的切线;
(2)解:由(1)知,∠E=∠DBE,∠DBE=∠ACD,∴∠E=∠ACD,∴AE=AC=AB=6.
在Rt△ABD中,AB=6,BD=8,∠ADE=∠ACB,∴sin∠ADB=![]() ,即sin∠ACB=
,即sin∠ACB=![]() ;
;
(3)证明:由(2)知,OA是△BDE的中位线,∴OA∥DE,OA=![]() DE.
DE.
∴△CDF∽△AOF,∴![]() ,∴CD=
,∴CD=![]() OA=
OA=![]() DE,即CD=
DE,即CD=![]() CE,∵AC=AE,AH⊥CE,
CE,∵AC=AE,AH⊥CE,
∴CH=HE=![]() CE,∴CD=
CE,∴CD=![]() CH,∴CD=DH.
CH,∴CD=DH.


科目:初中数学 来源: 题型:
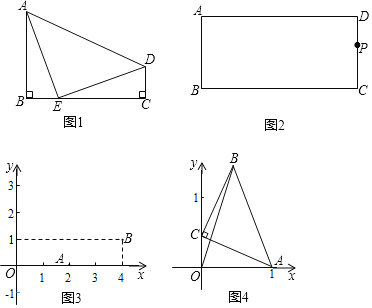
【题目】(初步探究)
(1)如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE、DE.判断△AED的形状,并说明理由.
(解决问题)
(2)如图2,在长方形ABCD中,点P是边CD上一点,在边BC、AD上分别作出点E、F,使得点F、E、P是一个等腰直角三角形的三个顶点,且PE=PF,∠FPE=90°.要求:仅用圆规作图,保留作图痕迹,不写作法.
(拓展应用)
(3)如图3,在平面直角坐标系xOy中,已知点A(2,0),点B(4,1),点C在第一象限内,若△ABC是等腰直角三角形,则点C的坐标是 .
(4)如图4,在平面直角坐标系xOy中,已知点A(1,0),点C是y轴上的动点,线段CA绕着点C按逆时针方向旋转90°至线段CB,CA=CB,连接BO、BA,则BO+BA的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据材料,解答问题
如图,数轴上有点![]() ,对应的数分别是6,-4,4,-1,则
,对应的数分别是6,-4,4,-1,则![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;
;![]() 两点间的距离为
两点间的距离为![]() ;由此,若数轴上任意两点
;由此,若数轴上任意两点![]() 分别表示的数是
分别表示的数是![]() ,则
,则![]() 两点间的距离可表示为
两点间的距离可表示为![]() .反之,
.反之,![]() 表示有理数
表示有理数![]() 在数轴上的对应点
在数轴上的对应点![]() 之间的距离,称之为绝对值的几何意义.
之间的距离,称之为绝对值的几何意义.

问题应用1:
(1)如果表示-1的点![]() 和表示
和表示![]() 的点
的点![]() 之间的距离是2,则点
之间的距离是2,则点![]() 对应的
对应的![]() 的值为___________;
的值为___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
问题应用2:
如图,若数轴上表示![]() 的点为
的点为![]() .
.
(4)![]() 的几何意义是数轴上_____________,当
的几何意义是数轴上_____________,当![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的几何意义是数轴上_______,
的几何意义是数轴上_______,![]() 的最小值是__________,此时点
的最小值是__________,此时点![]() 在数轴上应位于__________上;
在数轴上应位于__________上;
(6)根据以上推理方法可求![]() 的最小值是___________,此时
的最小值是___________,此时![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
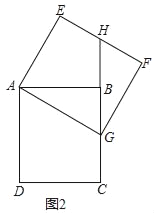
(1)求证:BH=EH;
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
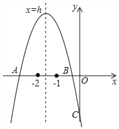
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的月历,图中带阴影的方框恰好盖住四个数,不改变带阴影的方框的形状大小,移动方框的位置.
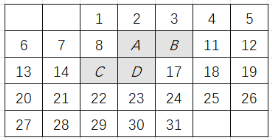
(1)若带阴影的方框盖住的4个数中,A表示的数是x,求这4个数的和(用含x的代数式表示);
(2)若带阴影的方框盖住的4个数之和为82,求出A表示的数;
(3)这4个数之和可能为38或112吗?如果可能,请求出这4个数,如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
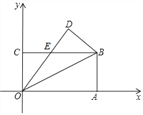
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(I)证明:EO=EB;
(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;
(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2015年年收入200美元,预计2017年年收入将达到1000美元,设2015年到2017年该地区居民年人均收入平均增长率为x,可列方程为![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com