
ЁОЬтФПЁПЃЈГѕВНЬНОПЃЉ
ЃЈ1ЃЉШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌЁЯBЃНЁЯCЃН90ЁуЃЌЕуEЪЧБпBCЩЯвЛЕуЃЌABЃНECЃЌBEЃНCDЃЌСЌНгAEЁЂDEЃЎХаЖЯЁїAEDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЃЈНтОіЮЪЬтЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌдкГЄЗНаЮABCDжаЃЌЕуPЪЧБпCDЩЯвЛЕуЃЌдкБпBCЁЂADЩЯЗжБ№зїГіЕуEЁЂFЃЌЪЙЕУЕуFЁЂEЁЂPЪЧвЛИіЕШбќжБНЧШ§НЧаЮЕФШ§ИіЖЅЕуЃЌЧвPEЃНPFЃЌЁЯFPEЃН90ЁуЃЎвЊЧѓЃКНігУдВЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЎ
ЃЈЭиеЙгІгУЃЉ
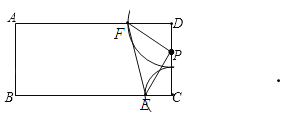
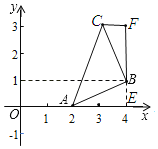
ЃЈ3ЃЉШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ4ЃЌ1ЃЉЃЌЕуCдкЕквЛЯѓЯоФкЃЌШєЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌдђЕуCЕФзјБъЪЧЁЁ ЁЁЃЎ
ЃЈ4ЃЉШчЭМ4ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЕуAЃЈ1ЃЌ0ЃЉЃЌЕуCЪЧyжсЩЯЕФЖЏЕуЃЌЯпЖЮCAШЦзХЕуCАДФцЪБеыЗНЯђа§зЊ90ЁужСЯпЖЮCBЃЌCAЃНCBЃЌСЌНгBOЁЂBAЃЌдђBO+BAЕФзюаЁжЕЪЧЁЁ ЁЁЃЎ
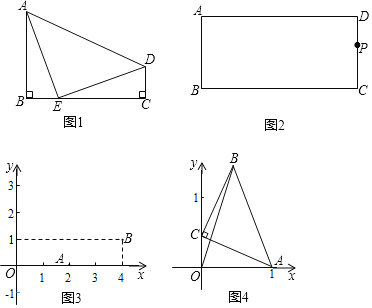
ЁОД№АИЁПЃЈ1ЃЉЁїAEDЪЧЕШбќжБНЧШ§НЧаЮЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉЃЈ1ЃЌ2ЃЉЁЂЃЈ3ЃЌ3ЃЉЁЂЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ4ЃЉ
ЃЉЃЛЃЈ4ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїЁїABEЁеЁїECD ЃЈSASЃЉЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉШчЭМЃЌвдЕуDЮЊдВаФCPГЄЮЊАыОЖзїЛЁНЛADгкЕуFЃЌвдЕуCЮЊдВаФЃЌDPГЄЮЊАыОЖзїЛЁНЛBEгкЕуEЃЌСЌНгEFЃЌEPЃЌFPЃЌЕуEЁЂFМДЮЊЫљЧѓЃЛ
ЃЈ3ЃЉЗжЁЯCAB=90ЁуЁЂЁЯABC=90ЁуЁЂЁЯACB=90ЁуЃЌШ§жжЧщПіЧѓНтМДПЩЃЛ
ЃЈ4ЃЉЧѓГіBЃЈmЃЌ1+mЃЉЃЌдђЃКBO+BA=![]() ЃЌBO+BAЕФжЕЯрЕБгкЧѓЕуPЃЈmЃЌmЃЉЕНЕуMЃЈ1ЃЌ-1ЃЉКЭЕуNЃЈ0ЃЌ-1ЃЉЕФзюаЁжЕЃЌМДПЩЧѓНтЃЎ
ЃЌBO+BAЕФжЕЯрЕБгкЧѓЕуPЃЈmЃЌmЃЉЕНЕуMЃЈ1ЃЌ-1ЃЉКЭЕуNЃЈ0ЃЌ-1ЃЉЕФзюаЁжЕЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁїAEDЪЧЕШбќжБНЧШ§НЧаЮЃЌ
жЄУїЃКЁпдкЁїABEКЭЁїECDжаЃЌ
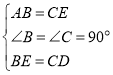 ,
,
ЁрЁїABEЁеЁїECD ЃЈSASЃЉ
ЁрAEЃНDEЃЌЁЯAEBЃНЁЯEDCЃЌ
ЁпдкRtЁїEDCжаЃЌЁЯCЃН90ЁуЃЌ
ЁрЁЯEDC+ЁЯDECЃН90ЁуЃЎ
ЁрЁЯAEB+ЁЯDECЃН90ЁуЃЎ
ЁпЁЯAEB+ЁЯDEC+ЁЯAEDЃН180ЁуЃЌ
ЁрЁЯAEDЃН90ЁуЃЎ
ЁрЁїAEDЪЧЕШбќжБНЧШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМЃЌвдЕуDЮЊдВаФCPГЄЮЊАыОЖзїЛЁНЛADгкЕуFЃЌвдЕуCЮЊдВаФЃЌDPГЄЮЊАыОЖзїЛЁНЛBEгкЕуEЃЌСЌНгEFЃЌEPЃЌFPЃЎ
ЁрЕуEЁЂFМДЮЊЫљЧѓЃЛ
ЃЈ3ЃЉШчЭМЃЌЕБЁЯCABЃН90ЁуЃЌCAЃНABЪБЃЌЙ§ЕуCзїCFЁЭAOгкЕуFЃЌЙ§ЕуBзїBEЁЭAOгкЕуEЃЌ
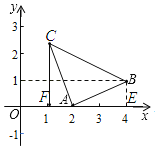
ЁпЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ4ЃЌ1ЃЉЃЌ
ЁрBEЃН1ЃЌOAЃН2ЃЌOEЃН4ЃЌЁрAEЃН2ЃЌ
ЁпЁЯCABЃН90ЁуЃЌBEЁЭAOЃЌ
ЁрЁЯCAF+ЁЯBAEЃН90ЁуЃЌЁЯBAE+ЁЯABEЃН90ЁуЃЌ
ЁрЁЯCAFЃНЁЯABEЃЌЧвACЃНABЃЌЁЯAFCЃНЁЯAEBЃН90ЁуЃЌ
ЁрЁїACFЁеЁїBAEЃЈAASЃЉ
ЁрCFЃНAEЃН2ЃЌAFЃНBEЃН1ЃЌ
ЁрOFЃНOAЉAFЃН1ЃЌ
ЁрЕуCзјБъЮЊЃЈ1ЃЌ2ЃЉ
ШчЭМЃЌЕБЁЯABCЃН90ЁуЃЌABЃНBCЪБЃЌЙ§ЕуBзїBEЁЭOAЃЌЙ§ЕуCзїCFЁЭBE
ЁпЁЯABCЃН90ЁуЃЌBEЁЭOAЃЌ
ЁрЁЯABE+ЁЯCBFЃН90ЁуЃЌЁЯABE+ЁЯBAEЃН90ЁуЃЌ
ЁрЁЯBAEЃНЁЯCBFЃЌЧвBCЃНABЃЌЁЯAEBЃНЁЯCFBЃН90Ёу
ЁрЁїBCFЁеЁїABEЃЈAASЃЉ
ЁрBEЃНCFЃН1ЃЌAEЃНBFЃН2ЃЌЁрEFЃН3
ЁрЕуCзјБъЮЊЃЈ3ЃЌ3ЃЉ
ШчЭМЃЌЕБЁЯACBЃН90ЁуЃЌCAЃНBCЪБЃЌЙ§ЕуCзїCDЁЭOAгкЕуDЃЌЙ§ЕуBзїBFЁЭCDгкЕуFЃЌ
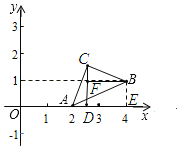
ЁпЁЯACD+ЁЯBCFЃН90ЁуЃЌЁЯACD+ЁЯCADЃН90ЁуЃЌ
ЁрЁЯBCFЃНЁЯCADЃЌЧвACЃНBCЃЌЁЯCDAЃНЁЯCFBЃЌ
ЁрЁїACDЁеЁїCBFЃЈAASЃЉ
ЁрCFЃНADЃЌBFЃНCDЃНDEЃЌ
ЁпAD+DEЃНAEЃН2
Ёр2ЃНAD+CDЃНAD+CF+DFЃН2AD+1
ЁрDAЃН![]() ЃЌ
ЃЌ
ЁрCDЃН![]() ЃЌODЃН
ЃЌODЃН![]() ЃЌ
ЃЌ
ЁрЕуCзјБъЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯЫљЪіЃКЕуCзјБъЮЊЃКЃЈ1ЃЌ2ЃЉЁЂЃЈ3ЃЌ3ЃЉЁЂЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЙЪД№АИЮЊЃКЃЈ1ЃЌ2ЃЉЁЂЃЈ3ЃЌ3ЃЉЁЂЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЃЈ4ЃЉШчЭМзїBHЁЭOHгкHЃЎ
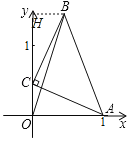
ЩшЕуCЕФзјБъЮЊЃЈ0ЃЌmЃЉЃЌ
гЩЃЈ1ЃЉжЊЃКOCЃНHBЃНmЃЌOAЃНHCЃН1ЃЌ
дђЕуBЃЈmЃЌ1+mЃЉЃЌ
дђЃКBO+BAЃН![]() ЃЌ
ЃЌ
BO+BAЕФжЕЃЌЯрЕБгкЧѓЕуPЃЈmЃЌmЃЉЕНЕуMЃЈ1ЃЌЉ1ЃЉКЭЕуNЃЈ0ЃЌЉ1ЃЉЕФзюаЁжЕЃЌ
ЯрЕБгкдкжБЯпyЃНxЩЯбАеввЛЕуPЃЈmЃЌmЃЉЃЌЪЙЕУЕуPЕНMЃЈ0ЃЌЉ1ЃЉЃЌЕНNЃЈ1ЃЌЉ1ЃЉЕФОрРыКЭзюаЁЃЌ
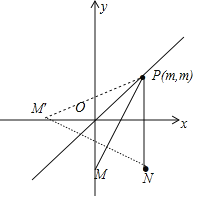
зїMЙигкжБЯпyЃНxЕФЖдГЦЕуMЁфЃЈЉ1ЃЌ0ЃЉЃЌ
взжЊPM+PNЃНPMЁф+PNЁнNMЁфЃЌ
MЁфNЃН![]() ЃЌ
ЃЌ
ЙЪЃКBO+BAЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкОиаЮABCDжа,AB=8,BC=4,НЋОиаЮбиACелЕў,ЕуBТфдкЕуB'ДІ,дђжиЕўВПЗж![]() ЕФУцЛ§ЮЊ()
ЕФУцЛ§ЮЊ()
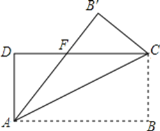
A.12B.10C.8D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцФквбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() КЭ
КЭ![]() ЕФЦНЗжЯпЃЌдђ
ЕФЦНЗжЯпЃЌдђ![]() ЕФЖШЪ§ЪЧ________ЃЎ
ЕФЖШЪ§ЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППЭдЫЙЋЫОЙцЖЈТУПЭПЩУтЗбаЏДјвЛЖЈжЪСПЕФааРюЃЌЕБааРюжЪСПГЌЙ§ЙцЖЈЪБЃЌашИЖЕФааРюЗбyЃЈдЊЃЉЪЧааРюжЪСПxЃЈkgЃЉЕФвЛДЮКЏЪ§ЃЌЧвВПЗжЖдгІЙиЯЕШчБэЫљЪОЃЎ
xЃЈkgЃЉ | Ё | 30 | 40 | 50 | Ё |
yЃЈдЊЃЉ | Ё | 4 | 6 | 8 | Ё |
ЃЈ1ЃЉЧѓyЙигкxЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЧѓТУПЭзюЖрПЩУтЗбаЏДјааРюЕФжЪСПЃЛ
ЃЈ3ЃЉЕБааРюЗб2ЁмyЁм7ЃЈдЊЃЉЪБЃЌПЩаЏДјааРюЕФжЪСПxЃЈkgЃЉЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтЃК
ЮвУЧжЊЕРЃЌЫФБпаЮОпгаВЛЮШЖЈадЃЌШнвзБфаЮЃЌШчЭМ1ЃЌвЛИіОиаЮЗЂЩњБфаЮКѓГЩЮЊвЛИіЦНааЫФБпаЮЃЌЩшетИіЦНааЫФБпаЮЯрСкСНИіФкНЧжаНЯаЁЕФвЛИіФкНЧЮЊІСЃЌЮвУЧАб![]() ЕФжЕНазіетИіЦНааЫФБпаЮЕФБфаЮЖШЃЎ
ЕФжЕНазіетИіЦНааЫФБпаЮЕФБфаЮЖШЃЎ
ЃЈ1ЃЉШєОиаЮЗЂЩњБфаЮКѓЕФЦНааЫФБпаЮгавЛИіФкНЧЪЧ120ЖШЃЌдђетИіЦНааЫФБпаЮЕФБфаЮЪЧЁЁ ЃЎ
ВТЯыжЄУїЃК
ЃЈ2ЃЉЩшОиаЮЕФУцЛ§ЮЊS1ЃЌЦфБфаЮКѓЕФЦНааЫФБпаЮУцЛ§ЮЊS2ЃЌЪдВТЯыS1ЃЌS2ЃЌ ![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЭиеЙЬНОПЃК
ЃЈ3ЃЉШчЭМ2ЃЌдкОиаЮABCDжаЃЌEЪЧADБпЩЯЕФвЛЕуЃЌЧвAB2=AEADЃЌетИіОиаЮЗЂЩњБфаЮКѓЮЊЦНааЫФБпаЮA1B1C1D1ЃЌE1ЮЊEЕФЖдгІЕуЃЌСЌНгB1E1ЃЌB1D1ЃЌШєОиаЮABCDЕФУцЛ§ЮЊ4![]() ЃЈmЃО0ЃЉЃЌЦНааЫФБпаЮA1B1C1D1ЕФУцЛ§ЮЊ2
ЃЈmЃО0ЃЉЃЌЦНааЫФБпаЮA1B1C1D1ЕФУцЛ§ЮЊ2![]() ЃЈmЃО0ЃЉЃЌЪдЧѓЁЯA1E1B1+ЁЯA1D1B1ЕФЖШЪ§ЃЎ
ЃЈmЃО0ЃЉЃЌЪдЧѓЁЯA1E1B1+ЁЯA1D1B1ЕФЖШЪ§ЃЎ
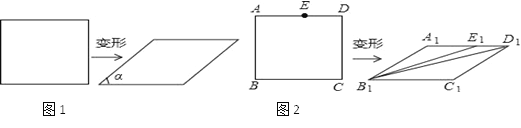
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮ![]() дкЦНУцжБНЧзјБъЯЕжаЃЌЦфжаШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ
дкЦНУцжБНЧзјБъЯЕжаЃЌЦфжаШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђЕкЫФИіЖЅЕуЕФзјБъЮЊ( )
ЃЌдђЕкЫФИіЖЅЕуЕФзјБъЮЊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
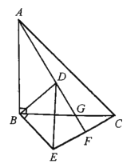
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШє![]() ШЦЕуBа§зЊЕН
ШЦЕуBа§зЊЕН![]() ЭтВПЃЌЦфЫћЬѕМўВЛБфЃЌдђЃЈ1ЃЉжаНсТлЪЧЗёШдГЩСЂЃПЧыжЄУїЃЎ
ЭтВПЃЌЦфЫћЬѕМўВЛБфЃЌдђЃЈ1ЃЉжаНсТлЪЧЗёШдГЩСЂЃПЧыжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпy1=kx+1ЃЈkЃМ0ЃЉгыжБЯпy2=mxЃЈmЃО0ЃЉЕФНЛЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() mЃЉЃЌдђВЛЕШЪНзщmxЉ2ЃМkx+1ЃМmxЕФНтМЏЮЊЃЈЁЁЁЁЃЉ
mЃЉЃЌдђВЛЕШЪНзщmxЉ2ЃМkx+1ЃМmxЕФНтМЏЮЊЃЈЁЁЁЁЃЉ
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЕФЖЅЕудкЁбOЩЯЃЌBDЪЧЁбOЕФжБОЖЃЌбгГЄCDЁЂBA НЛгкЕуEЃЌСЌНгACЁЂBDНЛгкЕуFЃЌзїAHЁЭCEЃЌДЙзуЮЊЕуHЃЌвбжЊЁЯADE=ЁЯACBЃЎ
ЃЈ1ЃЉЧѓжЄЃКAHЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєOB=4ЃЌAC=6ЃЌЧѓsinЁЯACBЕФжЕЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓжЄЃКCD=DHЃЎ
ЃЌЧѓжЄЃКCD=DHЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com