
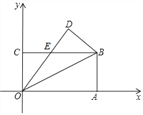
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(I)证明:EO=EB;
(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;
(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.
【答案】(I)证明见解析;(Ⅱ)P的坐标为(4,2)或(![]() ,
,![]() )或P(﹣
)或P(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );(Ⅲ)
);(Ⅲ)![]() .
.
【解析】分析:(Ⅰ)由折叠得到∠DOB=∠AOB,再由BC∥OA得到∠OBC=∠AOB,即∠OBC=∠DOB,即可;
(Ⅱ)设出点P坐标,分三种情况讨论计算即可;
(Ⅲ)根据题意判断出过点D作OA的垂线交OB于M,OA于N,求出DN即可.
详解:(Ⅰ)∵将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E,
∴∠DOB=∠AOB,
∵BC∥OA,
∴∠OBC=∠AOB,
∴∠OBC=∠DOB,
∴EO=EB;
(Ⅱ)∵点B的坐标为(8,4),
∴直线OB解析式为y=![]() x,
x,
∵点P是直线OB上的任意一点,
∴设P(a,![]() a).
a).
∵O(0,0),C(0,4),
∴OC=4,PO2=a2+(![]() a)2=
a)2=![]() a2,PC2=a2+(4-
a2,PC2=a2+(4-![]() a)2.
a)2.
当△OPC是等腰三角形时,可分三种情况进行讨论:
①如果PO=PC,那么PO2=PC2,
则![]() a2=a2+(4-
a2=a2+(4-![]() a)2,解得a=4,即P(4,2);
a)2,解得a=4,即P(4,2);
②如果PO=OC,那么PO2=OC2,
则![]() a2=16,解得a=±
a2=16,解得a=±![]() ,即P(
,即P(![]() ,
,![]() )或P(-
)或P(-![]() ,-
,-![]() );
);
③如果PC=OC时,那么PC2=OC2,
则a2+(4-![]() a)2=16,解得a=0(舍),或a=
a)2=16,解得a=0(舍),或a=![]() ,即P(
,即P(![]() ,
,![]() );
);
故满足条件的点P的坐标为(4,2)或(![]() ,
,![]() )或P(-
)或P(-![]() ,-
,-![]() )或(
)或(![]() ,
,![]() );
);
(Ⅲ)如图,过点D作OA的垂线交OB于M,交OA于N,
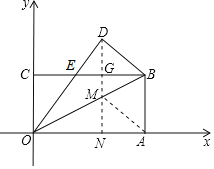
此时的M,N是AM+MN的最小值的位置,求出DN就是AM+MN的最小值.
由(1)有,EO=EB,
∵长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),
设OE=x,则DE=8-x,
在Rt△BDE中,BD=4,根据勾股定理得,DB2+DE2=BE2,
∴16+(8-x)2=x2,
∴x=5,
∴BE=5,
∴CE=3,
∴DE=3,BE=5,BD=4,
∵S△BDE=![]() DE×BD=
DE×BD=![]() BE×DG,
BE×DG,
∴DG=![]() ,
,
由题意有,GN=OC=4,
∴DN=DG+GN=![]() +4=
+4=![]() .
.
即:AM+MN的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA 交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示整数a,且![]() ,点B表示a的相反数.
,点B表示a的相反数.
(1)画数轴,并在数轴上标出点A与点B;
(2)点P, Q 在线段AB上,且点P在点Q的左侧,若P, Q两点沿数轴相向匀速运动,出发后经4秒两点相遇. 已知在相遇时点Q比点P多行驶了3个单位,相遇后经1秒点Q到达点P的起始位置. 问点P、Q运动的速度分别是每秒多少个单位;.
(3)在(2)的条件下,若点P从整数点出发,当运动时间为t秒时(t是整数),将数轴折叠,使A点与B点重合,经过折叠P点与Q点也恰好重合,求P点的起始位置表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
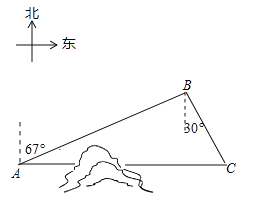
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点A按顺时针方向旋转得到
绕点A按顺时针方向旋转得到![]() 旋转角为
旋转角为![]() ,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当
,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当![]() 时,点P与点C之间的距离是________.
时,点P与点C之间的距离是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;
(3)当![]() 时,代数式
时,代数式![]() 的值为m,求当
的值为m,求当![]() 时,求代数式
时,求代数式![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
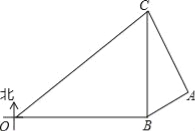
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
查看答案和解析>>
科目:初中数学 来源: 题型:
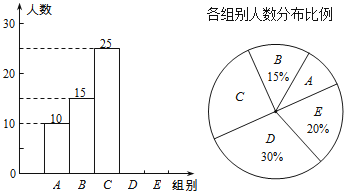
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个![]() 随机抽取了部分学生的听写结果,绘制成如下的图表.
随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
根据以上信息完成下列问题:
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______,并补全条形统计图;
______,并补全条形统计图;
![]() 扇形统计图中“C组”所对应的圆心角的度数是______;
扇形统计图中“C组”所对应的圆心角的度数是______;
![]() 已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com