
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点A按顺时针方向旋转得到
绕点A按顺时针方向旋转得到![]() 旋转角为
旋转角为![]() ,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当
,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当![]() 时,点P与点C之间的距离是________.
时,点P与点C之间的距离是________.
【答案】3或17.
【解析】
由旋转的性质可知△ACB≌△AED,推出∠CAB=∠EAD=∠CBA,则当∠DAF=∠CBA时,分两种情况,一种是A,F,E三点在同一直线上,另一种是 D,A,C在同一条直线上,可分别求出CP的长度.
解:∵AC=BC=10,
∴∠CAB=∠CBA,
由旋转的性质知,△ACB≌△AED,
∴AE=AC=10,∠CAB=∠EAD=∠CBA,
①∵∠DAF=∠CBA,
∴∠DAF=∠EAD,
∴A,F,E三点在同一直线上,如图1所示,
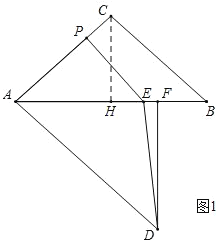
过点C作CH⊥AB于H,
则AH=BH=![]() AB=7,
AB=7,
∵EP⊥AC,
∴∠EPA=∠CHA=90°,
又∵∠CAH=∠EAP,CA=EA,
∴△CAH≌△EAP(AAS),
∴AP=AH=7,
∴PC=AC-AP=10-7=3;
②当D,A,C在同一条直线上时,如图2,
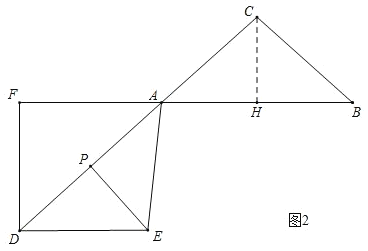
∠DAF=∠CAB=∠CBA,
此时AP=![]() AD=
AD=![]() AB=7,
AB=7,
∴PC=AC+AP=10+7=17.
故答案为:3或17.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像交x轴、y轴于A、B两点
的图像交x轴、y轴于A、B两点
(1)直接写出A、B两点的坐标:____________;______________。
(2)P为线段AB上一点,PQ//y轴交x轴于C,交双曲线![]() 于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
① 求k的值和P点坐标;
② 将△OBP绕点O逆时针旋转一周,在整个旋转过程中,P点能否落在双曲线![]() 上?请说明理由.
上?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
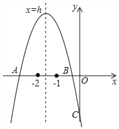
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的函数解析式为
的函数解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() .
.
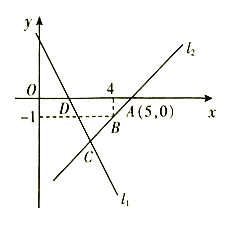
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍?如果存在,请求出
倍?如果存在,请求出![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
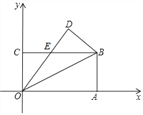
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(I)证明:EO=EB;
(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;
(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
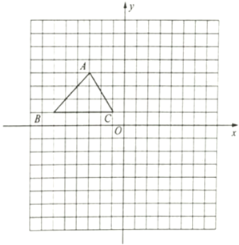
(1)画出![]() 关于原点中心对称的
关于原点中心对称的![]() ,其中A,B,C的对应点分别为
,其中A,B,C的对应点分别为![]() ,
,![]() ,
,![]() ;
;
(2)在(1)的基础上,将![]() 向上平移4个单位长度,画出平移后的
向上平移4个单位长度,画出平移后的![]() ,并写出
,并写出![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(3)D为y轴上一点,且![]() 是以AB为直角边的直角三角形.请直接写出D点的坐标.
是以AB为直角边的直角三角形.请直接写出D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
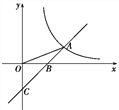
【题目】如图,已知直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=![]() 的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
的图象在第一象限交于点A,连接OA,若S△AOB∶S△BOC=1∶2,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把顺序连结四边形各边中点所得的四边形叫中点四边形。
(1)任意四边形的中点四边形是什么形状?为什么?
(2)符合什么条件的四边形,它的中点四边形是菱形?
(3)符合什么条件的四边形,它的中点四边形是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
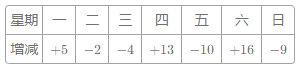
(1)产量最多的一天比产量最少的一天多生产 辆?
(2)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖20元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com