
【题目】如图,一次函数![]() 的图像交x轴、y轴于A、B两点
的图像交x轴、y轴于A、B两点
(1)直接写出A、B两点的坐标:____________;______________。
(2)P为线段AB上一点,PQ//y轴交x轴于C,交双曲线![]() 于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
① 求k的值和P点坐标;
② 将△OBP绕点O逆时针旋转一周,在整个旋转过程中,P点能否落在双曲线![]() 上?请说明理由.
上?请说明理由.

【答案】 (4,0) (0,-2)
【解析】分析:(1)利用图象与坐标轴交点坐标求法分别求出A,B两点坐标即可;
(2)①根据![]() 的面积为3,得出
的面积为3,得出![]() ,即可得出
,即可得出![]() ,再利用
,再利用![]() 得出QC与OC的长,即可得出P点坐标;
得出QC与OC的长,即可得出P点坐标;
②作第一象限角的角平分线OD,交反比例函数![]() 的图象于点D,首先得出OE2=6,以及OD2=12,进而得出OP>OD,即可得出答案.
的图象于点D,首先得出OE2=6,以及OD2=12,进而得出OP>OD,即可得出答案.
详解:(1)∵一次函数![]() 的图象分别交x轴、y轴于A.B两点,
的图象分别交x轴、y轴于A.B两点,
∴当图象与x轴相交,y=0时,0=![]() ,解得:x=4,
,解得:x=4,
当图象与y轴相交,x=0时,y=2,
故A(4,0),B(0,2);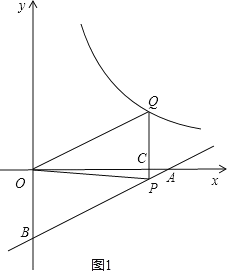
(2)①∵△OQC的面积为3,∴OC×CQ=6,∴k=6,
在平行四边形OBPQ中,OB//QP,OB=QP,OQ//AB,
∴∠QCO=∠BOA,∠QOC=∠BAO,
∴△QCO∽△BOA,
∴![]() ,∴OC=2QC,
,∴OC=2QC,
∵OC×CQ=6,
∴![]()
∴点P的坐标为![]()
②在Rt△OCP中,![]()
作第一象限角的角平分线OD,交反比例函数![]() 的图象于点D,
的图象于点D,
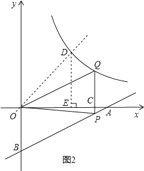
则OD的长是点O到反比例函数![]() 的图象上各点的最短距离,
的图象上各点的最短距离,
过点D作DE⊥OA于点E,
则![]()
∴![]()
∴OP>OD,
∴旋转后点P′能在反比例函数![]() 的图象上.
的图象上.


科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,引射线OC(点C在∠AOB外),若∠BOC=α(0°<α<90°),
OD平∠BOC,OE平∠AOD.
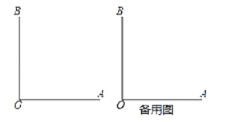
(1)若α=40°,请依题意补全图形,并求∠BOE的度数;
(2)请根据∠BOC=α,求出∠BOE的度数(用含α的表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”
设每只雀重x斤,每只燕重y斤,可列方程组为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
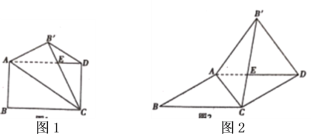
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
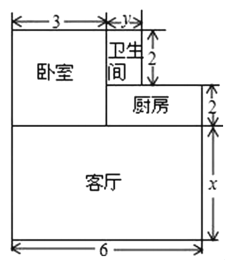
【题目】小张在贵阳购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:![]() ),解答下列问题:
),解答下列问题:
(1)用含![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)若![]() ,铺
,铺![]() 地砖的平均费用为140元,那么铺地砖的总费用为多少元?
地砖的平均费用为140元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
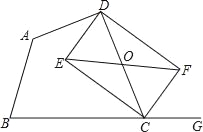
【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点A按顺时针方向旋转得到
绕点A按顺时针方向旋转得到![]() 旋转角为
旋转角为![]() ,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当
,点B,点C的对应点分别为点D,点E,过点D作直线AB的垂线,垂足为F,过点E作直线AC的垂线,垂足为P,当![]() 时,点P与点C之间的距离是________.
时,点P与点C之间的距离是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com