
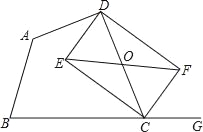
【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
【答案】证明见解析
【解析】试题分析:(1)由角平分线的定义及平行线的性质可证得∠DCE=∠FEC,∠EFC=∠DCF,则可求得OE=OC=OF;
(2)利用(1)的结论,结合条件可证得四边形DECF为平行四边形,再利用角平分线的定义可求得∠ECF为直角,则可证得四边形DECF为矩形.
试题解析:解:(1)∵CE平分∠BCD、CF平分∠GCD,∴∠BCE=∠DCE,∠DCF=∠GCF.
∵EF∥BC,∴∠BCE=∠FEC,∠EFC=∠GCF,∴∠DCE=∠FEC,∠EFC=∠DCF,∴OE=OC,OF=OC,∴OE=OF;
(2)∵点O为CD的中点,∴OD=OC.又∵OE=OF,∴四边形DECF是平行四边形.
∵CE平分∠BCD、CF平分∠GCD,∴∠DCE=![]() ∠BCD,∠DCF=
∠BCD,∠DCF=![]() ∠DCG,∴∠DCE+∠DCF=
∠DCG,∴∠DCE+∠DCF=![]() (∠BCD+∠DCG)=90°,即∠ECF=90°,∴四边形DECF是矩形.
(∠BCD+∠DCG)=90°,即∠ECF=90°,∴四边形DECF是矩形.


科目:初中数学 来源: 题型:
【题目】春节期间,七(1)班的李平、王丽等同学随家长一同到某公园游玩,下面是购买门票时,李平与他爸爸的对话(如图),试根据图中的信息,解答下列问题:

⑴李平他们一共去了几个成人,几个学生?
⑵请你帮助算一算,用哪种方式购票更省钱?说明理由.
⑶购完票后,李平发现七⑵班的张明等8名同学和他们的12名家长共20人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像交x轴、y轴于A、B两点
的图像交x轴、y轴于A、B两点
(1)直接写出A、B两点的坐标:____________;______________。
(2)P为线段AB上一点,PQ//y轴交x轴于C,交双曲线![]() 于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
① 求k的值和P点坐标;
② 将△OBP绕点O逆时针旋转一周,在整个旋转过程中,P点能否落在双曲线![]() 上?请说明理由.
上?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
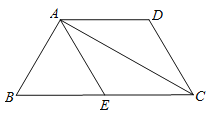
(1)求证:四边形AECD是平行四边形;
(2)当∠B=2∠DCA时,求证四边形AECD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
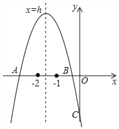
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的函数解析式为
的函数解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() .
.
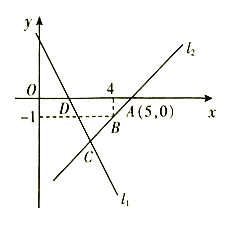
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍?如果存在,请求出
倍?如果存在,请求出![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把顺序连结四边形各边中点所得的四边形叫中点四边形。
(1)任意四边形的中点四边形是什么形状?为什么?
(2)符合什么条件的四边形,它的中点四边形是菱形?
(3)符合什么条件的四边形,它的中点四边形是矩形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com