
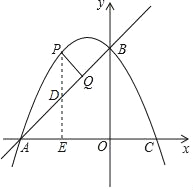
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.

【答案】(1)y=﹣x2﹣x+2;(2)﹣2<x<0;(3)P点坐标为(﹣1,2).
【解析】分析:(1)、根据题意得出点A和点B的坐标,然后利用待定系数法求出二次函数的解析式;(2)、根据函数图像得出不等式的解集;(3)、作PE⊥x轴于点E,交AB于点D,根据题意得出∠PDQ=∠ADE=45°,PD=![]() =1,然后设点P(x,﹣x2﹣x+2),则点D(x,x+2),根据PD的长度得出x的值,从而得出点P的坐标.
=1,然后设点P(x,﹣x2﹣x+2),则点D(x,x+2),根据PD的长度得出x的值,从而得出点P的坐标.
详解:(1)当y=0时,x+2=0,解得x=﹣2,当x=0时,y=0+2=2,
则点A(﹣2,0),B(0,2),
把A(﹣2,0),C(1,0),B(0,2),分别代入y=ax2+bx+c得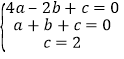 ,解得
,解得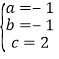 .
.
∴该抛物线的解析式为y=﹣x2﹣x+2;
(2)ax2+(b﹣1)x+c>2,ax2+bx+c>x+2,
则不等式ax2+(b﹣1)x+c>2的解集为﹣2<x<0;
(3)如图,作PE⊥x轴于点E,交AB于点D,
在Rt△OAB中,∵OA=OB=2,∴∠OAB=45°,∴∠PDQ=∠ADE=45°,
在Rt△PDQ中,∠DPQ=∠PDQ=45°,PQ=DQ=![]() ,∴PD=
,∴PD=![]() =1,
=1,
设点P(x,﹣x2﹣x+2),则点D(x,x+2),∴PD=﹣x2﹣x+2﹣(x+2)=﹣x2﹣2x,
即﹣x2﹣2x=1,解得x=﹣1,则﹣x2﹣x+2=2,∴P点坐标为(﹣1,2).


科目:初中数学 来源: 题型:
【题目】为进一步弘扬中华优秀传统文化,某校决定开展以下四项活动:A经典古诗文朗诵;B书画作品鉴赏;C民族乐器表演;D围棋赛![]() 学校要求学生全员参与,且每人限报一项
学校要求学生全员参与,且每人限报一项![]() 九年级
九年级![]() 班班长根据本班报名结果,绘制出了如下两个尚不完整的统计图,请结合图中信息解答下列问题:
班班长根据本班报名结果,绘制出了如下两个尚不完整的统计图,请结合图中信息解答下列问题: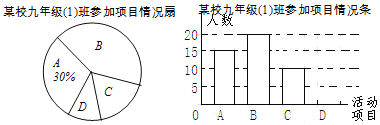
![]() 直接填空:九年级
直接填空:九年级![]() 班的学生人数是______,在扇形统计图中,B项目所对应的扇形的圆心角度数是______;
班的学生人数是______,在扇形统计图中,B项目所对应的扇形的圆心角度数是______;
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 用列表或画树状图的方法,求该班学生小聪和小明参加相同项目活动的概率.
用列表或画树状图的方法,求该班学生小聪和小明参加相同项目活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片![]() 沿对角线
沿对角线![]() 翻折,使点
翻折,使点![]() 的对应点
的对应点![]() (落在矩形
(落在矩形![]() 所在平面内,
所在平面内,![]() 与
与![]() 相交于点
相交于点![]() ,接
,接![]() .
.
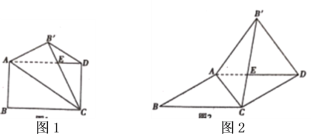
(1)在图1中,
①![]() 和
和![]() 的位置关系为__________________;
的位置关系为__________________;
②将![]() 剪下后展开,得到的图形是_________________;
剪下后展开,得到的图形是_________________;
(2)若图1中的矩形变为平行四边形时(![]() ),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,梯形ABCD中,AD∥BC,E是BC的中点,∠BEA=∠DEA ,联结AE、BD相交于点F,BD⊥CD.

(1)求证:AE=CD;
(2)求证:四边形ABED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
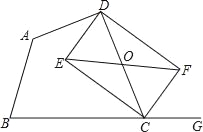
【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
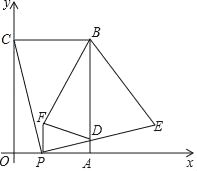
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=![]() ,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
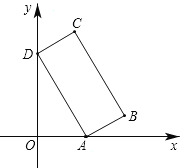
(1)求点B的坐标;
(2)求直线AB的解析式;
(3)在直线AB上是否存在点M,使以点C、点B、点M为顶点的三角形与△OAD相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com