
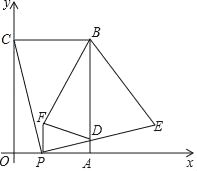
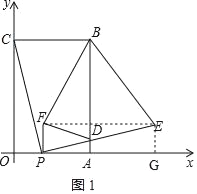
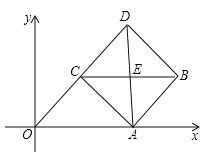
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
【答案】(1)、(t+6,t);(2)、当t=2时,S有最小值是16;(3)、理由见解析.
【解析】分析:(1)、过点E作EG⊥x轴于点G,根据题意得出CO=AB=6、OA=BC=4、OP=t,然后通过角之间的关系证明△PCO和△EPG全等,从而得出答案;(2)、根据DA∥EG得出△PAD和△PGE相似,求出AD的长度,然后根据四边形的面积等于△BDF的面积加上△BDE的面积得出函数解析式,从而求出面积的最值;(3)、根据∠FBD、∠FDB、∠BFD分别为直角,证明是否存在即可得出答案.
详解:(1)如图所示,过点E作EG⊥x轴于点G,则∠COP=∠PGE=90°,
由题意知CO=AB=6、OA=BC=4、OP=t,∵PE⊥CP、PF⊥OP,
∴∠CPE=∠FPG=90°,即∠CPF+∠FPE=∠FPE+∠EPG,∴∠CPF=∠EPG,
又∵CO⊥OG、FP⊥OG,∴CO∥FP,∴∠CPF=∠PCO,∴∠PCO=∠EPG,
在△PCO和△EPG中,∵∠PCO=∠EPG,∠POC=∠EGP,PC=EP,∴△PCO≌△EPG(AAS),
∴CO=PG=6、OP=EG=t,则OG=OP+PG=6+t,则点E的坐标为(t+6,t),
(2)∵DA∥EG,∴△PAD∽△PGE,∴![]() ,∴
,∴![]() ,∴AD=
,∴AD=![]() t(4﹣t),
t(4﹣t),
∴BD=AB﹣AD=6﹣![]() t(4﹣t)=
t(4﹣t)=![]() t2﹣
t2﹣![]() t+6,∵EG⊥x轴、FP⊥x轴,且EG=FP,
t+6,∵EG⊥x轴、FP⊥x轴,且EG=FP,
∴四边形EGPF为矩形,∴EF⊥BD,EF=PG,
∴S四边形BEDF=S△BDF+S△BDE=![]() ×BD×EF=
×BD×EF=![]() ×(
×(![]() t2﹣
t2﹣![]() t+6)×6=
t+6)×6=![]() (t﹣2)2+16,
(t﹣2)2+16,
∴当t=2时,S有最小值是16;
(3)①假设∠FBD为直角,则点F在直线BC上∵PF=OP<AB,
∴点F不可能在BC上,即∠FBD不可能为直角;
②假设∠FDB为直角,则点F在EF上,∵点D在矩形的对角线PE上,
∴点D不可能在EF上,即∠FDB不可能为直角;
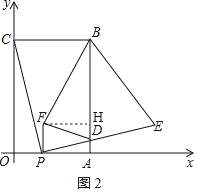
③假设∠BFD为直角且FB=FD,则∠FBD=∠FDB=45°如图2,作FH⊥BD于点H,
则FH=PA,即4﹣t=6﹣t,方程无解,
∴假设不成立,即△BDF不可能是等腰直角三角形.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某销售商计划购进甲、乙两种商品共![]() 件进行销售.已知甲种商品每件进价
件进行销售.已知甲种商品每件进价![]() 元,乙种商品每件进价
元,乙种商品每件进价![]() 元;通过市场考察,销售商决定甲种商品以每件
元;通过市场考察,销售商决定甲种商品以每件![]() 元的价格出售,乙种商品以每件
元的价格出售,乙种商品以每件![]() 元的价格出售.设销售商购进的甲种商品有
元的价格出售.设销售商购进的甲种商品有![]() 件,销售完甲、乙两种商品后获得的总利润为
件,销售完甲、乙两种商品后获得的总利润为![]() 元
元
![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 如果销售商购进的甲种商品的数量不少于乙种商品数量的
如果销售商购进的甲种商品的数量不少于乙种商品数量的![]() 倍,请求出获利最大的进货方案,所获得的最大利润是多少元?
倍,请求出获利最大的进货方案,所获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用大小和形状完全相同的小正方体木块搭成一-个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
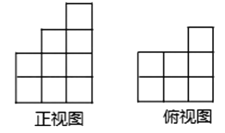
A.22个B.19个C.16个D.13个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
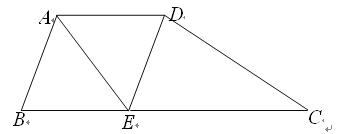
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
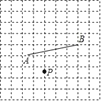
【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点A、P分别为小正方形的中点,B为格点.
(I)线段AB的长度等于_____;
(Ⅱ)在线段AB上存在一个点Q,使得点Q满足∠PQA=45°,请你借助给定的网格,并利用不带刻度的直尺作出∠PQA,并简要说明你是怎么找到点Q的:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组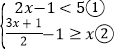
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]()
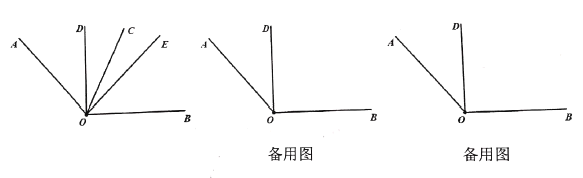
(1)求![]() ;
;
(2)![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转
的速度逆时针方向旋转![]() 秒(
秒(![]() ),
),![]() 为何值时
为何值时![]() ;
;
(3)射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,射线
的速度逆时针方向旋转,射线![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度顺时针方向旋转,若射线
的速度顺时针方向旋转,若射线![]() 同时开始旋转
同时开始旋转![]() 秒(
秒(![]() )后得到
)后得到![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.
(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com