
【题目】已知:如图,梯形ABCD中,AD∥BC,E是BC的中点,∠BEA=∠DEA ,联结AE、BD相交于点F,BD⊥CD.

(1)求证:AE=CD;
(2)求证:四边形ABED是菱形.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据直角三角形斜边上的中线的性质得到BE=DE=EC,根据等腰三角形的性质得到EF⊥BD,即EA∥CD,得到平行四边形AECD,即可得到答案;
(2)由(1)知:平行四边形AECD,推出AD=EC,推出AD=BE,根据平行四边形的判定得出平行四边形ABED,再根据菱形的判定即可得出答案.
证明:(1)∵BD⊥CD,
∴∠BDC=90°,
∵E是BC的中点,
∴BE=DE=EC,
∵∠BEA=∠DEA,
∴EF⊥BD,
∴∠BFE=90°,
∴EA∥CD,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AE=CD.
(2)∵四边形AECD是平行四边形,
∴AD=EC,
∴AD=BE,又AD∥BE,
∴四边形ABED是平行四边形,
∵BE=DE,
∴四边形ABED是菱形.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路步数达到10000步及以上可通过微信运动和腾讯基金会向公益活动捐款,如果步数在10000步及以上,每步可捐0.0002元;若步数在10000步以下,则不能参与捐款.
(1)老赵某天的步数为13000步,则他当日可捐多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐了8.4元,且甲的步数=乙的步数=丙步数的3倍,则丙走了多少步?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用大小和形状完全相同的小正方体木块搭成一-个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
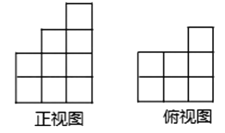
A.22个B.19个C.16个D.13个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
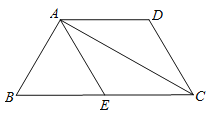
(1)求证:四边形AECD是平行四边形;
(2)当∠B=2∠DCA时,求证四边形AECD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
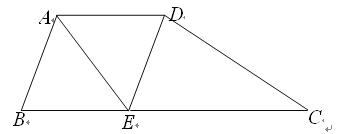
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°,CE=2BE,试判断△CDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组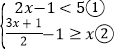
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com