
【题目】如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=![]() ,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
,线段AD、AB的长分别是方程x2﹣11x+24=0的两根(AD>AB).
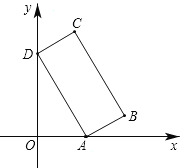
(1)求点B的坐标;
(2)求直线AB的解析式;
(3)在直线AB上是否存在点M,使以点C、点B、点M为顶点的三角形与△OAD相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)B点的坐标为(4+![]() ,
,![]() ).
).
(2)直线AB的解析式为y=![]() x﹣
x﹣![]()
(3)M3(﹣8+![]() ,
,![]() ﹣4
﹣4![]() ),M4(
),M4(![]() ,
,![]() ﹣
﹣![]() ).
).
【解析】
试题分析:(1)首先求出AD、AB,根据sin∠OAD=![]() 推出∠DAO=60°,作BE⊥x轴于点E,在RT△ABE中,即可解决问题.
推出∠DAO=60°,作BE⊥x轴于点E,在RT△ABE中,即可解决问题.
(2)利用待定系数法设直线AB为y=kx+b,把A、B坐标代入即可解决问题.
(3)分四种情形,利用相似三角形的性质求出AM的长,即可求出点M坐标.
试题解析:(1)作BE⊥x轴于点E,
解方程x2﹣11x+24=0得x1=3,x2=8.
∵AD>AB∴AD=8,AB=3,
∵sin∠OAD=![]() ,∴∠OAD=60°,∴∠BAE=30°,OA=AD×cos60°=4,
,∴∠OAD=60°,∴∠BAE=30°,OA=AD×cos60°=4,
∴AE=AB×cos30°=3×![]() =
=![]() ,BE=AB×sin30°=
,BE=AB×sin30°=![]() ,
,
∴B点的坐标为(4+![]() ,
,![]() ).
).
(2)设直线AB的解析式为y=kx+b(k≠0).
则 ,解得
,解得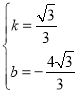
∴直线AB的解析式为y=![]() x﹣
x﹣![]()
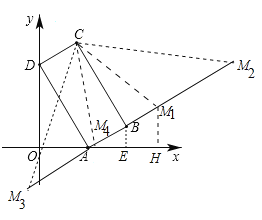
(3)存在,如图,①当△BCM1∽△ODA时,![]() ,
,
∴![]() ,∴BM1=
,∴BM1=![]() ,∴AM1=3+
,∴AM1=3+![]()
作M1H⊥OA于H,
∵∠M1AH=30°,∴HM1=![]() +
+![]() ,AH=
,AH=![]() +4,OH=8+
+4,OH=8+![]() ,∴点M1(8+
,∴点M1(8+![]() ,
,![]() +
+![]() ),
),
②当△CBM2∽△AOD时,![]() ,∴BM2=8
,∴BM2=8![]() ,∴AM2=3+8
,∴AM2=3+8![]() ,∴M2坐标为(16+
,∴M2坐标为(16+![]() ,
,![]() +4
+4![]() ),
),
根据对称性得到M3(﹣8+![]() ,
,![]() ﹣4
﹣4![]() ),M4(
),M4(![]() ,
,![]() ﹣
﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于原点中心对称的
关于原点中心对称的![]() ,其中A,B,C的对应点分别为
,其中A,B,C的对应点分别为![]() ,
,![]() ,
,![]() ;
;
(2)在(1)的基础上,将![]() 向上平移4个单位长度,画出平移后的
向上平移4个单位长度,画出平移后的![]() ,并写出
,并写出![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(3)D为y轴上一点,且![]() 是以AB为直角边的直角三角形.请直接写出D点的坐标.
是以AB为直角边的直角三角形.请直接写出D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
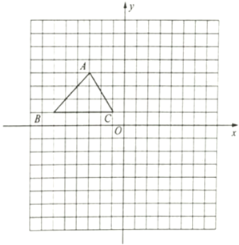
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把顺序连结四边形各边中点所得的四边形叫中点四边形。
(1)任意四边形的中点四边形是什么形状?为什么?
(2)符合什么条件的四边形,它的中点四边形是菱形?
(3)符合什么条件的四边形,它的中点四边形是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的边OA在x轴上,将平行四边形沿对角线AC对折,AO的对应线段为AD,且点D,C,O在同一条直线上,AD与BC交于点E.
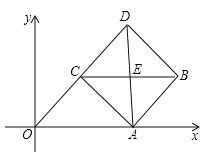
(1)求证:△ABC≌△CDA.
(2)若直线AB的函数表达式为![]() ,求三角线ACE的面积.
,求三角线ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,算做第一层,第二层每边两个点,第三层每边三个点,以此类推.

(1)填写下表:
层数 |
|
|
|
|
|
该层对应的点数 |
|
|
| ________ | ________ |
(2)写出第![]() 层对应的点数(
层对应的点数(![]() );
);
查看答案和解析>>
科目:初中数学 来源: 题型:
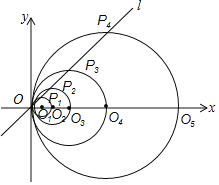
【题目】如图,在平面直角坐标系中,直线l的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ;
;![]() 按此做法进行下去,其中
按此做法进行下去,其中![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
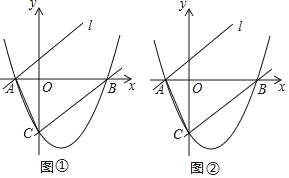
【题目】如图所示,抛物线y=![]() ﹣
﹣![]() x﹣4与x轴交于点A、B,与y 轴相交于点C.
x﹣4与x轴交于点A、B,与y 轴相交于点C.
(1)求直线BC的解析式;
(2)将直线BC向上平移后经过点A得到直线l:y=mx+n,点D在直线l上,若以A、B、C、D为顶点的四边形是平行四边形,求出点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com