
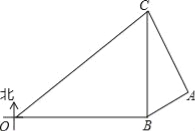
����Ŀ����ij�κ��Ͼ���ѧϰ�ڼ䣬�Ҿ�Ϊȷ����OBC�����ڵİ�ȫ������Dz���Ҿ����ֱ���O��B��C�������OBC�������״���ʾͼ�ϣ�����B�ھ���O����������80���ﴦ������C�ھ���B����������60���ﴦ�����Ҿ�����װ������ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩
��1�������Ҿ���Ҫ����OBC���������ä���أ����״����Ч̽��뾶r����Ϊ���ٺ��
��2������һ�ҵн�A�Ӷ����ӽ���OBC������ijһʱ�̾���B���Aλ�ڱ�ƫ��60�������ϣ�ͬʱ����C���Aλ����ƫ��30�������ϣ����ʱ�н�A����OBC�������̾���Ϊ���ٺ��
��3�����н�A����̾����·����20![]() ����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
���𰸡���1���״����Ч̽��뾶r����Ϊ50�����2���н�A����OBC�������̾���Ϊ15![]() �����3��B�����ٶ�����Ϊ20����/Сʱ��
�����3��B�����ٶ�����Ϊ20����/Сʱ��
��������
�����������1����RT��OBC�У����ݹ��ɶ������OC��������r��![]() OC���ɴ˵ô𰸣���2����AM��BC��M�������AB�ij�����RT��ABM�����AM�ij����ɵô𰸣���3������B�����ڵ�N�����ص��н�����BM��ȡһ��H��ʹ��HB=HN����MN=x�����г��������x�������BN��AN���ò���ʽ������⣮
OC���ɴ˵ô𰸣���2����AM��BC��M�������AB�ij�����RT��ABM�����AM�ij����ɵô𰸣���3������B�����ڵ�N�����ص��н�����BM��ȡһ��H��ʹ��HB=HN����MN=x�����г��������x�������BN��AN���ò���ʽ������⣮
�����������1����RT��OBC����BO=80��BC=60����OBC=90����
��OC=![]() ��
��
��![]() OC=
OC=![]() ��100=50
��100=50
���״����Ч̽��뾶r����Ϊ50���
��2����AM��BC��M��
�ߡ�ACB=30������CBA=60����
���CAB=90����
��AB=![]() BC=30��
BC=30��
��RT��ABM�У��ߡ�AMB=90����AB=30����BAM=30����
��BM=![]() AB=15��AM=
AB=15��AM=![]() BM=15
BM=15![]() ��
��
����ʱ�н�A����OBC�������̾���Ϊ15![]() ���
���
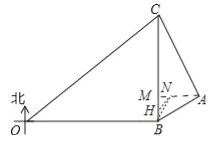
��3������B�����ڵ�N�����ص��н�����BM��ȡһ��H��ʹ��HB=HN����MN=x��
�ߡ�HBN=��HNB=15����
���MHN=��HBN+��HNB=30����
��HN=HB=2x��MH=![]() x��
x��
��BM=15��
��15=![]() x+2x��
x+2x��
x=30��15![]() ��
��
��AN=30![]() ��30��
��30��
BN=![]() ����B�����ٶ�Ϊa����/Сʱ��
����B�����ٶ�Ϊa����/Сʱ��
������![]() ��
��
��a��20��
��B�����ٶ�����Ϊ20����/Сʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η�����,�����������ʵ��������( )
A.x2=-x
B.x2+4x+4=0
C.x2+2=2x
D.(x-1) 2+2=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OP��QR��ST�������и�ʽ����ȷ���ǣ������� 
A.��1+��2+��3=180��
B.��1+��2����3=90��
C.��1����2+��3=90��
D.��2+��3����1=180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͨ��ij��������¶���8�棬������������5�棬����������������£���ҹ�����½���7�棬������ҹ����¶����森
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ų����εIJ���������6���ˣ�������ͼ�ķ�ʽ�ڷŲ��������ӣ�
��1���۲�������ݹ��������
�������� | 1 | 2 | 3 | 4 | ��n |
�������� | 6 | 8 | 10 |
��2��һ�Ҿ�¥������ͼ�ķ�ʽƴ����Ҫʹƴ�ɵ�һ�Ŵ�����պ�����160�ˣ������輸�Ų���ƴ��һ�Ŵ������
��3�����Ƶ���240�����Ͳͣ�����ƴ���ķ�ʽ���ã�����Ҫ�ö����Ų�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������¶��壺��һ���ı����д����������ߵ�ƽ���͵���һ���Խ��ߵ�ƽ������Ƹ��ı���Ϊ�����ı��Σ�
��1�������ı����У��ǹ����ı��ε�Ϊ ������д��ż��ɣ�
�پ��Σ�����һ����Ϊֱ�ǵ������ı��Σ�����һ����Ϊ60�������Σ�
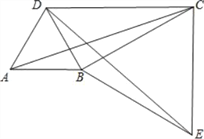
��2����ͼ������ABC�ƶ���B��˳ʱ�뷽����ת60���õ���DBE����DCB=30��������AD��DC��CE��
����֤����BCE�ǵȱ������Σ�
����֤���ı���ABCD�ǹ����ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
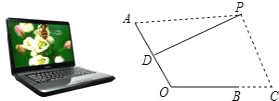
����Ŀ����ͼ��һ̨������ˮƽ�����ϵıʼDZ����ԣ����������������ͼ��ʾ�ļ���ͼ�Σ�����ʾ��������IJ��AO�����������IJ��BO����Ϊ24cm����PΪ�۾�����λ�ã�DΪAO���е㣬����PD����PD?AOʱ���Ƶ�PΪ������ӽǵ�������PC?BC������C��OB���ӳ����ϣ���BC=12cm��
��1����PA=45cmʱ����PC�ij���
��2����?AOC=120��ʱ��������ӽǵ���P��ֱ��PC�ϵ�λ�ûᷢ��ʲô�仯����ʱPC�ij��Ƕ��٣���ͨ������˵�����������ȷ��0.1cm�����ÿ�ѧ���������ο����ݣ� ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е�.![]()
��1����AC ��9cm��CB �� 6 cm�����߶�MN�ij���
��2����CΪ�߶�AB����һ�㣬����AC��CB �� ![]() cm�������������䣬���ܲ���MN�ij����𣿲�˵������.������һ����Ļ������㷢�ֵĽ�����
cm�������������䣬���ܲ���MN�ij����𣿲�˵������.������һ����Ļ������㷢�ֵĽ�����
��3����C���߶�AB���ӳ����ϣ�������AC ![]() BC �� b cm��M��N�ֱ�ΪAC��BC���е㣬���ܲ���MN�ij������뻭��ͼ�Σ�д����Ľ��ۣ���˵������.
BC �� b cm��M��N�ֱ�ΪAC��BC���е㣬���ܲ���MN�ij������뻭��ͼ�Σ�д����Ľ��ۣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
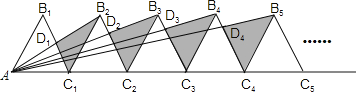
����Ŀ����ͼ����n+1�����߳�Ϊ2�ĵȱ���������һ������ͬһֱ���ϣ�����B2D1C1�����ΪS1����B3D2C2�����ΪS2��������B��n+1��DnCn�����ΪSn����Sn=____���ú�n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com