
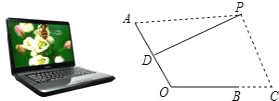
����Ŀ����ͼ��һ̨������ˮƽ�����ϵıʼDZ����ԣ����������������ͼ��ʾ�ļ���ͼ�Σ�����ʾ��������IJ��AO�����������IJ��BO����Ϊ24cm����PΪ�۾�����λ�ã�DΪAO���е㣬����PD����PD?AOʱ���Ƶ�PΪ������ӽǵ�������PC?BC������C��OB���ӳ����ϣ���BC=12cm��
��1����PA=45cmʱ����PC�ij���
��2����?AOC=120��ʱ��������ӽǵ���P��ֱ��PC�ϵ�λ�ûᷢ��ʲô�仯����ʱPC�ij��Ƕ��٣���ͨ������˵�����������ȷ��0.1cm�����ÿ�ѧ���������ο����ݣ� ![]() ��
�� ![]() ��
��
���𰸡���1��27cm����2��λ�������ˣ�34.7cm.
�������������������1������PO�������߶δ�ֱƽ���ߵ����ʵó�PO=PA=45cm����OC=OB+BC=12+24=36cm��Ȼ�����ù��ɶ����������PC=![]() =27cm����2����D��DE��OC��BO�ӳ�����E����D��DF��PC��F�����ı���DECF�Ǿ��Σ��Ƚ�Rt��DOE�����DE=DOsin60��=6
=27cm����2����D��DE��OC��BO�ӳ�����E����D��DF��PC��F�����ı���DECF�Ǿ��Σ��Ƚ�Rt��DOE�����DE=DOsin60��=6![]() ��EO=
��EO=![]() DO=6����FC=DE=6
DO=6����FC=DE=6![]() ��DF=EC=EO+OB+BC=42���ٽ�Rt��PDF�����PF=DFtan30��=42��
��DF=EC=EO+OB+BC=42���ٽ�Rt��PDF�����PF=DFtan30��=42��![]() =14
=14![]() ����PC=PF+FC=14
����PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ��34.68��27�����ɵó����ۣ�
��34.68��27�����ɵó����ۣ�
�����������1����PA=45cmʱ������PO����ͼ��
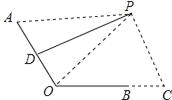 ��DΪAO���е㣬PD��AO����PO=PA=45cm����BO=24cm��BC=12cm����C=90������OC=OB+BC=36cm��PC=
��DΪAO���е㣬PD��AO����PO=PA=45cm����BO=24cm��BC=12cm����C=90������OC=OB+BC=36cm��PC=![]() =27cm����2������AOC=120������D��DE��OC��BO�ӳ�����E����D��DF��PC��F����ͼ��
=27cm����2������AOC=120������D��DE��OC��BO�ӳ�����E����D��DF��PC��F����ͼ��
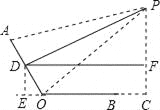 �����ı���DECF�Ǿ��Σ���Rt��DOE�У��ߡ�DOE=60����DO=
�����ı���DECF�Ǿ��Σ���Rt��DOE�У��ߡ�DOE=60����DO=![]() AO=12��
AO=12��
��DE=DOsin60��=6![]() ��EO=
��EO=![]() DO=6����FC=DE=6
DO=6����FC=DE=6![]() ��DF=EC=EO+OB+BC=6+24+12=42����Rt��PDF�У��ߡ�PDF=30������PF=DFtan30��=42��
��DF=EC=EO+OB+BC=6+24+12=42����Rt��PDF�У��ߡ�PDF=30������PF=DFtan30��=42��![]() =14
=14![]() ����PC=PF+FC=14
����PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ��34.68cm��27cm������P��ֱ��PC�ϵ�λ�������ˣ�
��34.68cm��27cm������P��ֱ��PC�ϵ�λ�������ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1����֪|a��1|����ab��2��2��0����a��b��2016��ֵ��
��2���ⷽ�̣� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж�����ijһ�����������ǩ�10�棬���������5�棬��һ����²�Ϊ�� ��
A.��5��
B.5��
C.10��
D.15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
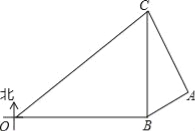
����Ŀ����ij�κ��Ͼ���ѧϰ�ڼ䣬�Ҿ�Ϊȷ����OBC�����ڵİ�ȫ������Dz���Ҿ����ֱ���O��B��C�������OBC�������״���ʾͼ�ϣ�����B�ھ���O����������80���ﴦ������C�ھ���B����������60���ﴦ�����Ҿ�����װ������ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩
��1�������Ҿ���Ҫ����OBC���������ä���أ����״����Ч̽��뾶r����Ϊ���ٺ��
��2������һ�ҵн�A�Ӷ����ӽ���OBC������ijһʱ�̾���B���Aλ�ڱ�ƫ��60�������ϣ�ͬʱ����C���Aλ����ƫ��30�������ϣ����ʱ�н�A����OBC�������̾���Ϊ���ٺ��
��3�����н�A����̾����·����20![]() ����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ε����Ʊ���1��4����ô���������������ε��ܳ����ǣ�������
A.2��1B.1��16C.1��4D.1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����У�һ�����ӿ���6�ˣ����������ְڷŷ�ʽ��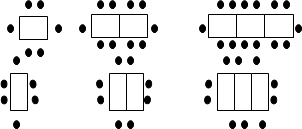
��1������n������ʱ�����ְڷŷ�ʽ�����������ˣ�
��2��һ���������Ҫ�Ӵ�98λ�˿�ͬ�Ͳͣ�������ֻ��25�������IJ�������������������ľ����������ѡ�����ַ�ʽ���ڷŲ�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����ѧ��2870�ˣ�ѧУΪ�˽�һ���ḻѧ�����������֯�������ȤС�������Ϊ��Уѧ���������һ������������飮���ݲɼ��������ݣ�������������ͳ��ͼ������������
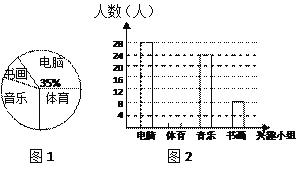
�������ͳ��ͼ1��2���ṩ����Ϣ������������⣺
��1��д��2���м�ֵ��Ϣ������������Ҫ�������Ϣ����
��2����γ�����������������Ƕ��٣���ͼ2�У��뽫����ͳ��ͼ�еġ����������ֵ�ͼ�β���������
��3�����á��黭��������ռ�����������İٷ����Ƕ��٣����Ƹ���ѧ���е�ѧ���У����á��黭����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������3+3+4+4������ͼ����ƽ��ֱ������ϵ�У�������![]() ������A��
������A��![]() ��0���͵�B��1��
��0���͵�B��1��![]() ������x�����һ������ΪC��
������x�����һ������ΪC��
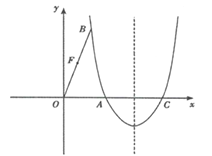
��1���������ߵı���ʽ����2����D�ڶԳ�����Ҳ࣬x���Ϸ����������ϣ���![]() �����D�����ꣻ
�����D�����ꣻ
��3������2���������£�����BD���������߶Գ����ڵ�E������AE
���ж��ı���OAEB����״����˵�����ɣ�
����F��OB���е㣬��M��ֱ��BD�ϵ�һ�����㣬�ҵ�M���B���غϣ���![]() ����ֱ��д���߶�BM�ij���
����ֱ��д���߶�BM�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com