
【题目】(本题3+3+4+4分)如图,在平面直角坐标系中,抛物线![]() 经过点A(
经过点A(![]() ,0)和点B(1,
,0)和点B(1,![]() ),与x轴的另一个交点为C,
),与x轴的另一个交点为C,
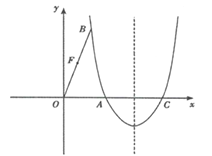
(1)求抛物线的表达式;(2)点D在对称轴的右侧,x轴上方的抛物线上,且![]() ,求点D的坐标;
,求点D的坐标;
(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE
①判断四边形OAEB的形状,并说明理由;
②点F是OB的中点,点M是直线BD上的一个动点,且点M与点B不重合,当![]() ,请直接写出线段BM的长。
,请直接写出线段BM的长。
【答案】(1)![]() ;(2)D(4,
;(2)D(4,![]() );(3)①四边形OAEB是平行四边形.理由如见解析②线段BM的长为
);(3)①四边形OAEB是平行四边形.理由如见解析②线段BM的长为![]() 或
或![]() .
.
【解析】
试题分析:(1)把点AB坐标分别代入解析式,然后解方程组即可求出抛物线的函数表达式;(2)由∠BDA=∠DAC,可知BD∥x轴,点B与点D纵坐标相同,解一元二次方程求出点D的坐标;(3)①由BE与OA平行且相等,可判定四边形OAEB为平行四边形;②点M在点B的左右两侧均有可能,因此分两种情况讨论.
试题解析:(1)把点A(![]() ,0)和点B(1,
,0)和点B(1,![]() )分别代入
)分别代入![]() 得:
得: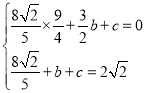 ,解得
,解得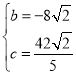 ,所以抛物线的函数表达式为
,所以抛物线的函数表达式为![]() ;(2)当∠BDA=∠DAC时, BD∥x轴,因为点B(1,
;(2)当∠BDA=∠DAC时, BD∥x轴,因为点B(1,![]() ),令y=
),令y= ![]() ,所以
,所以![]() ,解得
,解得![]() ,所以D(4,
,所以D(4,![]() );(3)①四边形OAEB为平行四边形.抛物线的对称轴是
);(3)①四边形OAEB为平行四边形.抛物线的对称轴是![]() ,所以BE=
,所以BE=![]() ,因为点A(
,因为点A(![]() ,0),所以OA=BE=
,0),所以OA=BE= ![]() ,又BE//OA,所以四边形OAEB为平行四边形;②点M在点B的左右两侧均有可能,需要分类讨论:∵O(0,0),B(1,
,又BE//OA,所以四边形OAEB为平行四边形;②点M在点B的左右两侧均有可能,需要分类讨论:∵O(0,0),B(1,![]() ),F为OB的中点,∴F(
),F为OB的中点,∴F(![]() ,
,![]() )。
)。
过点F作FN⊥直线BD于点N,则FN=![]() ﹣
﹣![]() =
=![]() ,BN=1﹣
,BN=1﹣![]() =
=![]() 。
。
在Rt△BNF中,由勾股定理得:![]() 。
。
∵∠BMF=![]() ∠MFO,∠MFO=∠FBM+∠BMF,∴∠FBM=2∠BMF。
∠MFO,∠MFO=∠FBM+∠BMF,∴∠FBM=2∠BMF。
(I)当点M位于点B右侧时.
在直线BD上点B左侧取一点G,使BG=BF=![]() ,连接FG,则GN=BG﹣BN=1,
,连接FG,则GN=BG﹣BN=1,
在Rt△FNG中,由勾股定理得:![]() 。
。
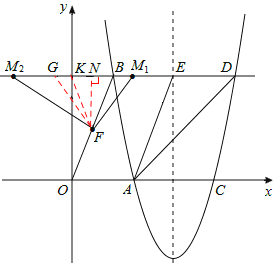
∵BG=BF,∴∠BGF=∠BFG。
又∵∠FBM=∠BGF+∠BFG=2∠BMF,
∴∠BFG=∠BMF。
又∵∠MGF=∠MGF,∴△GFB∽△GMF。
∴![]() ,即
,即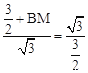 。
。
∴BM=![]() 。
。
(II)当点M位于点B左侧时,
设BD与y轴交于点K,连接FK,则FK为Rt△KOB斜边上的中线,
∴KF=![]() OB=FB=
OB=FB=![]() 。∴∠FKB=∠FBM=2∠BMF。
。∴∠FKB=∠FBM=2∠BMF。
又∵∠FKB=∠BMF+∠MFK,∴∠BMF=∠MFK。∴MK=KF=![]() 。
。
∴BM=MK+BK=![]() +1=
+1=![]() 。
。
综上所述,线段BM的长为![]() 或
或![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
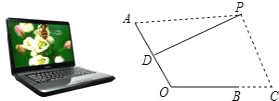
【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线AC于点G,且DE=DG;
(1)求证:AE=CG;
(2)求证:BE∥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
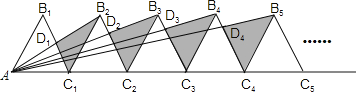
【题目】如图,(n+1)个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△B(n+1)DnCn的面积为Sn,则Sn=____(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
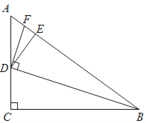
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+ax+b的图象与y轴交于点A(0,-2),与x轴交于点B(1,0)和点C,D(m,0)(m>2)是x轴上一点.
(1)求二次函数的解析式;
(2)点E是第四象限内的一点,若以点D为直角顶点的Rt△CDE与以A,O,B为顶点的三角形相似,求点E坐标(用含m的代数式表示);
(3)在(2)的条件下,抛物线上是否存在一点F,使得四边形BCEF为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com