
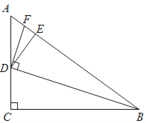
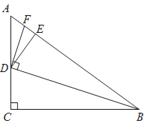
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
【答案】(1)证明见解析;(2)AD2=AF·AB,理由见解析;(3)5+2![]() .
.
【解析】试题解析:(1)根据题意得∠ADF+∠BDC=∠EDF+∠BDE=90°,由折叠可知,∠BDE=∠BDC.所以∠ADF=∠EDF;
(2)易证△ADF∽△ABD,得AF∶AD=AD∶AB=DF∶DB,得AD2=AF·AB;
(3)设AE=x,DE=![]() x,由勾股定理可得,AD=DE=
x,由勾股定理可得,AD=DE=![]() x,可证△ADE∽△DFE,得BE=2x2,由(2)知AD2=AF·AB,即3x2=(x-1)×(x+2x2).解得x 的值,即可求BC的值
x,可证△ADE∽△DFE,得BE=2x2,由(2)知AD2=AF·AB,即3x2=(x-1)×(x+2x2).解得x 的值,即可求BC的值
试题解析:(1)∵DF⊥DB,∴∠BDF=90°.
∴∠ADF+∠BDC=∠EDF+∠BDE=90°
由折叠可知,∠BDE=∠BDC.
∴∠ADF=∠EDF.
(2)AD,AF,AB之间的数量关系为AD2=AF·AB,理由如下:
由折叠可知,∠DEF=∠BFD=∠C=90°.
∴∠EDF+∠DFE=∠ABD+∠DFE=90°.
∴∠EDF=∠ABD.
∴∠ADF=∠DBA.
∵∠A=∠A,∴△ADF∽△ABD.
∴AF∶AD=AD∶AB=DF∶DB.
∴AD2=AF·AB.
(3)在Rt△ADE中,tanA=DE∶AE=![]() ∶1,则可设AE=x,DE=
∶1,则可设AE=x,DE=![]() x,由勾股定理可得,AD=DE=
x,由勾股定理可得,AD=DE=![]() x.
x.
∵∠ABD=∠EDF,∠AED=∠DEF,
∴△ADE∽△DFE. ∴DE∶EF=BE∶DE,即DE2=EF·EB.
∴(![]() x)2=1×BE,即BE=2x2。
x)2=1×BE,即BE=2x2。
由(2)知AD2=AF·AB,
∴(![]() x)2=(AE-EF)(AE+BE)=(x-1)×(x+2x2).
x)2=(AE-EF)(AE+BE)=(x-1)×(x+2x2).
即3x2=(x-1)×(x+2x2).
解得,x=1+![]() ,x=1-
,x=1-![]() (舍).
(舍).
∴BE=2x2=2(1+![]() )2=5+2
)2=5+2![]() .
.
由折叠可知,BC=BE=5+2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式: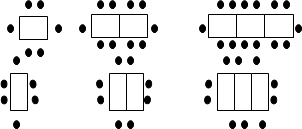
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中属于必然事件的是( )
A.任意买一张电影票,座位号是偶数B.367人中至少有2人的生日相同
C.掷一次骰子,向上的一面是5点D.某射击运动员射击1次,命中靶心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题3+3+4+4分)如图,在平面直角坐标系中,抛物线![]() 经过点A(
经过点A(![]() ,0)和点B(1,
,0)和点B(1,![]() ),与x轴的另一个交点为C,
),与x轴的另一个交点为C,
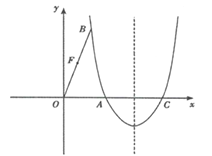
(1)求抛物线的表达式;(2)点D在对称轴的右侧,x轴上方的抛物线上,且![]() ,求点D的坐标;
,求点D的坐标;
(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE
①判断四边形OAEB的形状,并说明理由;
②点F是OB的中点,点M是直线BD上的一个动点,且点M与点B不重合,当![]() ,请直接写出线段BM的长。
,请直接写出线段BM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
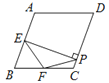
A. 55° B. 50° C. 45° D. 35°
查看答案和解析>>
科目:初中数学 来源: 题型:
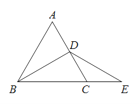
【题目】如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD.
(1)用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);
(2)若AB=2,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在操场上活动时,小明发现旗杆的影子与旁边的树的影子好像平行,但他不敢确定,那么他可以采取的最好办法是( )
A. 通过平移的办法进行验证
B. 看看其他同学是不是这样认为
C. 构造并测量两个同位角,若相等则影子平行
D. 构造几何模型,用已学知识证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师给42名学生每人买了一件纪念品,其中有:每支12元的钢笔,每把4元的圆规,每册16元的词典,共用了216元,则陈老师买了钢笔支,词典册;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com