
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线AC于点G,且DE=DG;
(1)求证:AE=CG;
(2)求证:BE∥DF.
【答案】证明:(1)∵DE=DG,
∴∠DEG=∠DGE,
∴∠AED=∠CGD,
∵四边形ABCD是正方形,
∴AD=CD=BC,∠DAC=∠BCE=∠DCA=45°,
在△ADE和△CDG中,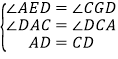 ,
,
∴△ADE≌△CDG(AAS),
∴AE=CG;
(2)在△BCE和△DCE中,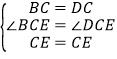 ,
,
∴△BCE≌△DCE (SAS),
∴∠BEC=∠DEG,
∴∠BEC=∠DGE,
∴BE∥DF.
【解析】(1)先证∠AED=∠CGD,再证明△ADE≌△CDG,根据全等三角形的对应边相等即可得出结论;
(2)先证明△BCE≌△DCE,得出对应角相等∠BEC=∠DEG,得出∠BEC=∠DGE,即可证出平行线.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式: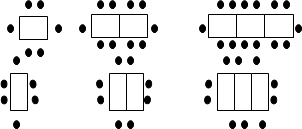
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有学生2870人,学校为了进一步丰富学生课余生活,组织调查各兴趣小组活动情况,为此校学生会进行了一次随机抽样调查.根据采集到的数据,绘制如下两个统计图(不完整):
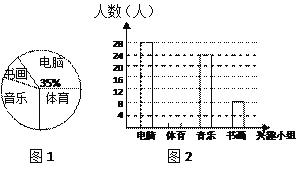
请你根据统计图1、2中提供的信息,解答下列问题:
(1)写出2条有价值信息(不包括下面要计算的信息);
(2)这次抽样调查的样本容量是多少?在图2中,请将条形统计图中的“体育”部分的图形补充完整;
(3)爱好“书画”的人数占被调查人数的百分数是多少?估计该中学现有的学生中,爱好“书画”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
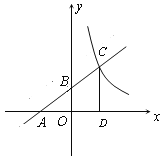
【题目】如图,已知一次函数![]() 的图像分别交x轴、y轴于A、B两点,且与反比例函数
的图像分别交x轴、y轴于A、B两点,且与反比例函数![]() (
( ![]() >0)的图像在第一象限交于点C(4,n),CD⊥x轴于D.
>0)的图像在第一象限交于点C(4,n),CD⊥x轴于D.
(1)求m、n的值;
(2)求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园“六·一”期间举行特优读书游园活动,成人票和儿童票均有较大折扣.张凯、李利都随他们的家人参加了本次活动.王斌也想去,就去打听张凯、李利买门票花了多少钱.张凯说他家去了3个大人和4个小孩,共花了38元钱;李利说他家去了4个大人和2个小孩,共花了44元钱,王斌家计划去3个大人和2个小孩,请你帮他计算一下,需准备元钱买门票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中属于必然事件的是( )
A.任意买一张电影票,座位号是偶数B.367人中至少有2人的生日相同
C.掷一次骰子,向上的一面是5点D.某射击运动员射击1次,命中靶心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题3+3+4+4分)如图,在平面直角坐标系中,抛物线![]() 经过点A(
经过点A(![]() ,0)和点B(1,
,0)和点B(1,![]() ),与x轴的另一个交点为C,
),与x轴的另一个交点为C,
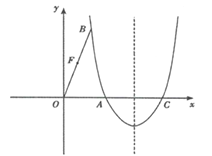
(1)求抛物线的表达式;(2)点D在对称轴的右侧,x轴上方的抛物线上,且![]() ,求点D的坐标;
,求点D的坐标;
(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE
①判断四边形OAEB的形状,并说明理由;
②点F是OB的中点,点M是直线BD上的一个动点,且点M与点B不重合,当![]() ,请直接写出线段BM的长。
,请直接写出线段BM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在操场上活动时,小明发现旗杆的影子与旁边的树的影子好像平行,但他不敢确定,那么他可以采取的最好办法是( )
A. 通过平移的办法进行验证
B. 看看其他同学是不是这样认为
C. 构造并测量两个同位角,若相等则影子平行
D. 构造几何模型,用已学知识证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com