
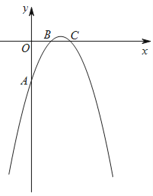
����Ŀ����֪���κ���y����x2��ax��b��ͼ����y�ύ�ڵ�A(0����2)����x�ύ�ڵ�B(1��0)�͵�C��D(m��0)(m��2)��x����һ�㣮
(1)����κ����Ľ���ʽ��
(2)��E�ǵ��������ڵ�һ�㣬���Ե�DΪֱ�Ƕ����Rt��CDE����A��O��BΪ��������������ƣ����E����(�ú�m�Ĵ���ʽ��ʾ)��
(3)��(2)�������£����������Ƿ����һ��F��ʹ���ı���BCEFΪƽ���ı��Σ������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3�����ڣ�
����3�����ڣ�![]()
�������������������1������A��1��0����B��2��0����C��0��-2��������κ���y=ax2+bx+c�У��з�������a��b��c���ɣ�
��2����ΪD��O�ֱ�Ϊ����ֱ�������εĶ��㣬�ɷ�Ϊ��EDB�ס�AOC����BDE�ס�AOC����������������Ʊ���ED��ȷ��E�����ꣻ
��3�������������ϴ���һ��F��ʹ���ı���ABEFΪƽ���ı��Σ�EF=AB=1����F�ĺ�����Ϊm-1����Ϊ�ٵ���E1������Ϊ��m�� ![]() ��ʱ����F1������Ϊ��m-1��
��ʱ����F1������Ϊ��m-1�� ![]() �����ڵ���E2������Ϊ��m��4-2m��ʱ����F2������Ϊ��m-1��4-2m��������������ֱ���������߽���ʽ��m��ֵ��ȷ��F������꣮
�����ڵ���E2������Ϊ��m��4-2m��ʱ����F2������Ϊ��m-1��4-2m��������������ֱ���������߽���ʽ��m��ֵ��ȷ��F������꣮
���������(1)�������⣬��![]() ����ã�a��3��b����2
����ã�a��3��b����2
![]() ��
��
��2����y��0ʱ���У�x2��3x��2��0����ã�x1��1��x2��2����OC��2.
�������AO��2��BO��1��CD��m��2.
��CDE�ס�AOC��ʱ����AO��CD��BO��DE��
�ࡡ2��(m��2)��1��DE.����DE��![]() .
.
�ߵ�![]() �ڵ������ޣ���E1��m��
�ڵ������ޣ���E1��m�� ![]() ����
����
����DEC�ס�AOC��ʱ����AO��ED��BO��CD��
��2��DE��1��(m��2).����DE��2m��4.
�ߵ�![]() �ڵ������ޣ���E2��m��4-2m��.
�ڵ������ޣ���E2��m��4-2m��.
��3�������������ϴ���һ��F��ʹ���ı���BCEFΪƽ���ı��Σ���EF��BC��1��
��F�ĺ�����Ϊm��1��
����![]() ������Ϊ
������Ϊ![]() ʱ����
ʱ����![]() ������Ϊ
������Ϊ![]()
�ߵ�![]() �������ߵ�ͼ���ϣ�
�������ߵ�ͼ���ϣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����ȥ����
����ȥ����
��![]() .
.
����![]() ������Ϊ
������Ϊ![]() ʱ����
ʱ����![]() ������Ϊ
������Ϊ![]() .
.
�ߵ�![]() �������ߵ�ͼ���ϣ�
�������ߵ�ͼ���ϣ�
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ����ȥ����
����ȥ����![]() ��
��
��![]() ��
��
��ʹ���ı���BCEFΪƽ���ı��εĵ�F������Ϊ![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����ѧ��2870�ˣ�ѧУΪ�˽�һ���ḻѧ�����������֯�������ȤС�������Ϊ��Уѧ���������һ������������飮���ݲɼ��������ݣ�������������ͳ��ͼ������������
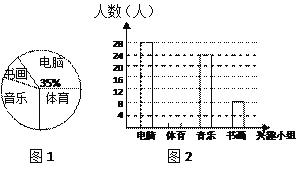
�������ͳ��ͼ1��2���ṩ����Ϣ������������⣺
��1��д��2���м�ֵ��Ϣ������������Ҫ�������Ϣ����
��2����γ�����������������Ƕ��٣���ͼ2�У��뽫����ͳ��ͼ�еġ����������ֵ�ͼ�β���������
��3�����á��黭��������ռ�����������İٷ����Ƕ��٣����Ƹ���ѧ���е�ѧ���У����á��黭����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������3+3+4+4������ͼ����ƽ��ֱ������ϵ�У�������![]() ������A��
������A��![]() ��0���͵�B��1��
��0���͵�B��1��![]() ������x�����һ������ΪC��
������x�����һ������ΪC��
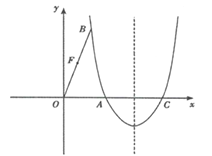
��1���������ߵı���ʽ����2����D�ڶԳ�����Ҳ࣬x���Ϸ����������ϣ���![]() �����D�����ꣻ
�����D�����ꣻ
��3������2���������£�����BD���������߶Գ����ڵ�E������AE
���ж��ı���OAEB����״����˵�����ɣ�
����F��OB���е㣬��M��ֱ��BD�ϵ�һ�����㣬�ҵ�M���B���غϣ���![]() ����ֱ��д���߶�BM�ij���
����ֱ��д���߶�BM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������M��3a��9��1+a���ǵڶ����ĵ㣬��a��ȡֵ��Χ�������ϱ�ʾ��ȷ���ǣ�������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
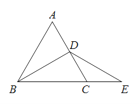
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��AC���е㣬�ӳ�BC��E��ʹCE��CD.
(1)�ó߹���ͼ�ķ���������D��DM��BE������ΪM(��д������ֻ������ͼ�ۼ�)��
(2)��AB��2����EM�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ε�һ�ڽ�ƽ���߰Ѿ��ε�һ���߷ֳ�3��5�����֣���þ��ε��ܳ��ǣ�������
A.16
B.22��16
C.26
D.22��26
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲٳ��ϻʱ��С��������˵�Ӱ�����Աߵ�����Ӱ�Ӻ���ƽ�У���������ȷ������ô�����Բ�ȡ����ð취��(����)
A. ͨ��ƽ�Ƶİ취������֤
B. ��������ͬѧ�Dz���������Ϊ
C. ���첢��������ͬλ�ǣ��������Ӱ��ƽ��
D. ���켸��ģ�ͣ�����ѧ֪ʶ֤��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90����D��F��AB���ϵ����㣬��DFΪֱ���ġ�O��BC�ཻ�ڵ�E������EF����OFE��![]() ��A.
��A.
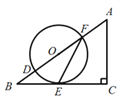
(1)��֤��BC�ǡ�O�����ߣ�
(2)��sinB��![]() �����FEC��
�����FEC��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com