
����Ŀ���������¶��壺��һ���ı����д����������ߵ�ƽ���͵���һ���Խ��ߵ�ƽ������Ƹ��ı���Ϊ�����ı��Σ�
��1�������ı����У��ǹ����ı��ε�Ϊ ������д��ż��ɣ�
�پ��Σ�����һ����Ϊֱ�ǵ������ı��Σ�����һ����Ϊ60�������Σ�
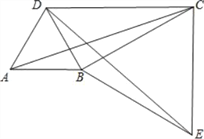
��2����ͼ������ABC�ƶ���B��˳ʱ�뷽����ת60���õ���DBE����DCB=30��������AD��DC��CE��
����֤����BCE�ǵȱ������Σ�
����֤���ı���ABCD�ǹ����ı��Σ�
���𰸡���1���٢�����2����֤������������֤��������
�������������������1���ɹ����ı��εĶ���������ı��ε����ʣ���ɵó���
��2��������ת�����ʿ�֪��ABC�ա�DBE���Ӷ��ɵ�BC=BE���ɡ�CBE=60���ɵ���BCEΪ�ȱ������Σ����ɢٿɵá�BCE=60�����Ӷ���֪��DCE��ֱ�������Σ������ù��ɶ������ɽ�����⣮
���������
��1������ͼ��
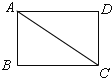
���ı���ABCD�Ǿ��Σ�
���B=90����
��AB2+BC2=AC2��
���������ǹ����ı��Σ�
����ͼ��
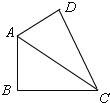
�ߡ�B=90����
��AB2+BC2=AC2��
������һ����Ϊֱ�ǵ��ı����ǹ����ı��Σ�
����һ����Ϊ60�������Σ��ڱ߱���û��ֱ�ǣ����Բ����㹴���ı��εĶ��壬
�ʴ�Ϊ�٢���
��2���١ߡ�ABC�Ƶ�B˳ʱ����ת��60������DBE��
��BC=BE����CBE=60����
������BCE��
BC=BE����CBE=60��
���BCE�ǵȱ������Σ�
�ڡߡ�BCE�ǵȱ������Σ�
��BC=CE����BCE=60����
�ߡ�DCB=30����
���DCE=��DCB+��BCE=90����
��Rt��DCE����DC2+CE2=DE2��
��DE=AC��BC=CE��
��DC2+BC2=AC2��
���ı���ABCD�ǹ����ı��Σ�


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д� ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й���������y=(x+1) 2+2��˵��,��ȷ����( )
A.��������
B.�Գ�����ֱ��x=1
C.��x=-1ʱ,y����Сֵ2
D.��x>-1ʱ,y��x���������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���P(��3��5)����y��ĶԳƵ��������(����)
A. (3��5) B. (3����5) C. (5����3) D. (��3����5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
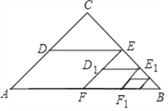
����Ŀ����ͼ,��ABC��,��C=90��,AC=BC=2,ȡBC���е�E,��ED��AB,EF��AC,�õ��ı���EDAF,�����������S1��ȡBE�е�E1����E1D1��FB��E1F1��EF,�õ��ı���E1D1FF1�������������S2���մ˹�������ȥ,��S1=_______��S2017=____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
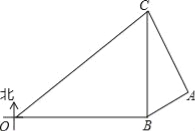
����Ŀ����ij�κ��Ͼ���ѧϰ�ڼ䣬�Ҿ�Ϊȷ����OBC�����ڵİ�ȫ������Dz���Ҿ����ֱ���O��B��C�������OBC�������״���ʾͼ�ϣ�����B�ھ���O����������80���ﴦ������C�ھ���B����������60���ﴦ�����Ҿ�����װ������ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩
��1�������Ҿ���Ҫ����OBC���������ä���أ����״����Ч̽��뾶r����Ϊ���ٺ��
��2������һ�ҵн�A�Ӷ����ӽ���OBC������ijһʱ�̾���B���Aλ�ڱ�ƫ��60�������ϣ�ͬʱ����C���Aλ����ƫ��30�������ϣ����ʱ�н�A����OBC�������̾���Ϊ���ٺ��
��3�����н�A����̾����·����20![]() ����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15���ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�AB=4��P���߶�AD�ϵĶ��㣬PE��AC�ڵ�E��PF��BD�ڵ�F����PE+PF��ֵΪ��������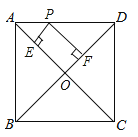
A.2![]()
B.4
C.4![]()
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ε����Ʊ���1��4����ô���������������ε��ܳ����ǣ�������
A.2��1B.1��16C.1��4D.1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺 ![]()
��2��������ֵ.2( ![]() ��5y)��[��3(
��5y)��[��3( ![]() ��3y)] ������
��3y)] ������ ![]() =
= ![]() ��y=-2
��y=-2
��3���ⷽ�̣� ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com