
【题目】如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )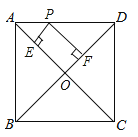
A.2![]()
B.4
C.4![]()
D.2
【答案】A
【解析】解:在正方形ABCD中,OA⊥OD,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△APE是等腰直角三角形,
∴PF=OE,PE=BE,
∴PE+PF=BE+OE=OA,
∵AB=BC=4,
∴OA=![]() AC=
AC=![]() x4
x4![]() =2
=2![]() ,
,
∴PE+PF=2![]() ,
,
故选A.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


科目:初中数学 来源: 题型:
【题目】下面数据是截至2010年费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35 31 31 37 32 38
36 31 39 32 38 37 34 29 34 38 32 35 36
33 29 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 40 31 38 38 40 40 37
小果、小冻、小甜将数据整理,分别按组距是2,5,10进行分组,列出频数分布表,画出频数分布直方图,如下

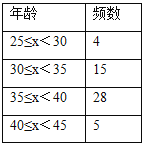
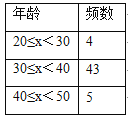
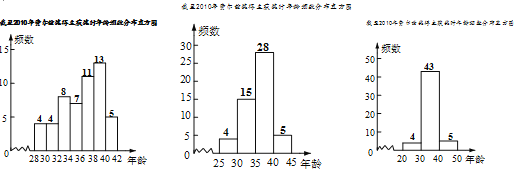
根据以上材料回答问题:
小果、小冻、小甜三人中,比较哪一位同学分组能更好的说明费尔兹奖得主获奖时的年龄分布,并简要说明其他两位同学分组的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0.其中正确结论的个数是( )
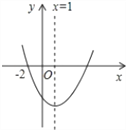
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
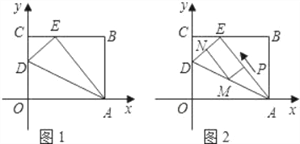
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
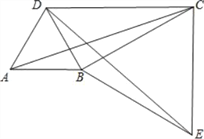
【题目】给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)以下四边形中,是勾股四边形的为 .(填写序号即可)
①矩形;②有一个角为直角的任意凸四边形;③有一个角为60°的菱形.
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,∠DCB=30°,连接AD,DC,CE.
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电话拨号上网有两种收费方式,用户可以任选其一:
A.计时制:0.05元每分钟;
B.包月制:60元每月(限一部个人住宅电话上网);
此外,每一种上网方式都得加收通信费0.02元每分钟.
(1)某用户某月上网的时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为25小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于提倡环保节能,自行车已成为市民日常出行的主要工具之一,据某自行车经销店4至6月份统计,某品牌自行车4月份销售200辆,6月份销售338辆,求该品牌自行车销售量的月平均增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com