
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.![]()
(1)若AC =9cm,CB = 6 cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB = ![]() cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
(3)若C在线段AB的延长线上,且满足AC ![]() BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
【答案】
(1)解: ∵AC=9cm,点M是AC的中点,∴CM= ![]() AC=4.5cm,∵BC=6cm,点N是BC的中点,∴CN=
AC=4.5cm,∵BC=6cm,点N是BC的中点,∴CN= ![]() BC=3cm,∴MN=CM+CN=7.5cm,∴线段MN的长度为7.5cm
BC=3cm,∴MN=CM+CN=7.5cm,∴线段MN的长度为7.5cm
(2)解: MN= ![]() a , 当C为线段AB上一点,且M , N分别是AC , BC的中点,则存在MN=
a , 当C为线段AB上一点,且M , N分别是AC , BC的中点,则存在MN= ![]() a
a
(3)解: 当点C在线段AB的延长线时,如图: ![]() 则AC>BC , ∵M是AC的中点,∴CM=
则AC>BC , ∵M是AC的中点,∴CM= ![]() AC , ∵点N是BC的中点,∴CN=
AC , ∵点N是BC的中点,∴CN= ![]() BC , ∴MN=CM-CN=
BC , ∴MN=CM-CN= ![]() (AC-BC)=
(AC-BC)= ![]() b
b
【解析】(1)根据中点的定义得出CM= ![]() AC , CN=
AC , CN= ![]() BC ,故MN=MC+NC=
BC ,故MN=MC+NC=![]() (AC+BC),代入数据计算即可;
(AC+BC),代入数据计算即可;
(2)由(1)得MN=MC+NC=![]() ×(AC+BC),而AC+BC=acm,可得出答案;
×(AC+BC),而AC+BC=acm,可得出答案;
(3)作出图后结合已知条件可知MC=![]() ×AC,NC=
×AC,NC=![]() BC,又因为MN=MC-NC=
BC,又因为MN=MC-NC=![]() (AC-BC)且AC-BC=bcm,即可得出答案.
(AC-BC)且AC-BC=bcm,即可得出答案.


科目:初中数学 来源: 题型:
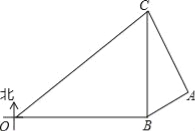
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式: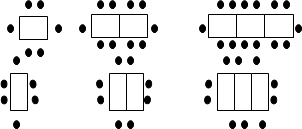
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有学生2870人,学校为了进一步丰富学生课余生活,组织调查各兴趣小组活动情况,为此校学生会进行了一次随机抽样调查.根据采集到的数据,绘制如下两个统计图(不完整):
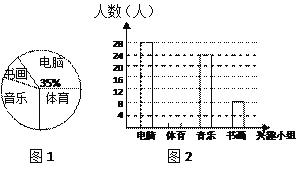
请你根据统计图1、2中提供的信息,解答下列问题:
(1)写出2条有价值信息(不包括下面要计算的信息);
(2)这次抽样调查的样本容量是多少?在图2中,请将条形统计图中的“体育”部分的图形补充完整;
(3)爱好“书画”的人数占被调查人数的百分数是多少?估计该中学现有的学生中,爱好“书画”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园“六·一”期间举行特优读书游园活动,成人票和儿童票均有较大折扣.张凯、李利都随他们的家人参加了本次活动.王斌也想去,就去打听张凯、李利买门票花了多少钱.张凯说他家去了3个大人和4个小孩,共花了38元钱;李利说他家去了4个大人和2个小孩,共花了44元钱,王斌家计划去3个大人和2个小孩,请你帮他计算一下,需准备元钱买门票.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com