
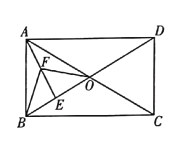
【题目】如图,矩形![]() 中,
中,![]() 对角线
对角线![]() 交于点
交于点![]() 为
为![]() 上任意点,
上任意点,![]() 为
为![]() 中点,则
中点,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
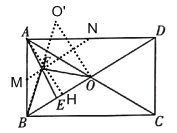
设M、N分别为AB、AD的中点,则MN是△ABD的中位线,点F在MN上,作点O关于MN的对称点O′,连接BO′,则BO′即为![]() 的最小值,易证△ABO是等边三角形,过点A作AH⊥BO于H,求出AH=OO′=
的最小值,易证△ABO是等边三角形,过点A作AH⊥BO于H,求出AH=OO′=![]() ,然后利用勾股定理求出BO′即可.
,然后利用勾股定理求出BO′即可.
解:如图,设M、N分别为AB、AD的中点,则MN是△ABD的中位线,
∵E为BD上任意点,F为AE中点,
∴点F在MN上,
作点O关于MN的对称点O′,连接BO′,则BO′即为![]() 的最小值,
的最小值,
∵四边形ABCD是矩形,![]() ,
,
∴OA=OB,∠AOB=60°,
∴△ABO是等边三角形,
∴AB=BO=4,
过点A作AH⊥BO于H,则BH=HO=2,
∴AH=![]() ,
,
∵MN∥BD,点H关于MN的对称点为A,点O关于MN的对称点为O′
∴OO′=AH=![]() ,且OO′⊥BD,
,且OO′⊥BD,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() ,
,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
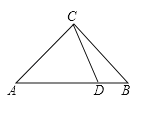
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点,连结CD,将线段CD绕点C逆时针旋转90°得到线段CE,连结DE,BE.
(1)依题意补全图形;
(2)若∠ACD=α,用含α的代数式表示∠DEB;
(3)若△ACD的外心在三角形的内部,请直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
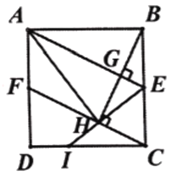
【题目】如图1,正方形![]() 中, 点
中, 点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
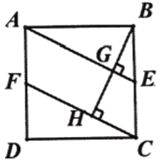
(2)如图2,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点I,
于点I,
①求证:![]() ;
;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 与函数
与函数![]() 定义新函数
定义新函数![]()
(1)若![]() 则新函数
则新函数![]() ;
;
(2)若新函数![]() 的解析式为
的解析式为![]() 则
则![]() ,
,![]() ;
;
(3)设新函数![]() 顶点为
顶点为![]() .
.
①当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值;
有最大值,并求出最大值;
②求![]() 与
与![]() 的函数解析式;
的函数解析式;
(4)请你探究:函数![]() 与新函数
与新函数![]() 分别经过定点
分别经过定点![]() ,函数
,函数![]() 的顶点为
的顶点为![]() ,新函数
,新函数![]() 上存在一点
上存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形为平行四边形时,直接写出
为顶点的四边形为平行四边形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
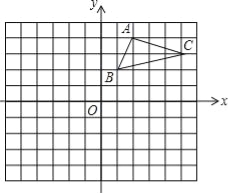
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
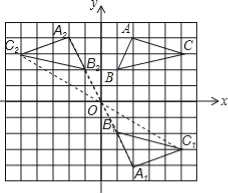
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
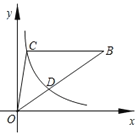
【题目】如图,△OBC的边BC∥x轴,过点C的双曲线y=![]() (k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
(k≠0)与△OBC的边OB交于点D,且OD:DB=1:2,若△OBC的面积等于8,则k的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
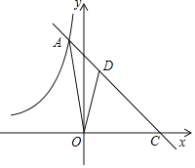
【题目】如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y=![]() (k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求k的值;
(2)根据图象,直接写出当x<0时不等式![]() >﹣x+5的解集;
>﹣x+5的解集;
(3)求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,杨树的杨絮漫天飞舞,易引发皮肤病、呼吸道疾病等,给人们生活造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(调查问卷如下),并根据调查结果绘制了如下尚不完整的统计图:
调查问卷
治理杨絮:您选哪一项? (每人只选一项)
A.减少杨树新增面积,控制杨树每年的栽种量;
B.调整树种结构,逐渐更换现有杨树;
C.选育无絮杨品种,并推广种植;
D.对杨树注射生物干扰素,避免产生飞絮;
E.其他.
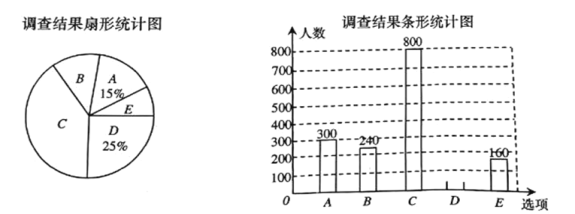
根据以上信息,解答下列问题:
(1)在扇形统计图中,求扇形![]() 的圆心角度数;
的圆心角度数;
(2)补全条形统计图;
(3)若该市约有![]() 万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与⊙O的位置关系,并说明理由.
(2)若AC=3,CD=2.5,求FG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com