
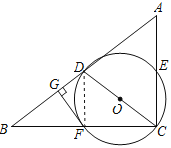
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与⊙O的位置关系,并说明理由.
(2)若AC=3,CD=2.5,求FG的长.

【答案】(1)FG与⊙O相切,理由见解析;(2)FG=![]() .
.
【解析】
(1)如图,连接OF,根据直角三角形斜边中线的性质可得CD=BD,即可得到∠DBC=∠DCB,根据等腰三角形的性质得到∠OFC=∠OCF,可得∠OFC=∠DBC,即可证明OF//DB,根据平行线的性质可推出∠OFG=90°,即可得到结论;
(2)连接DF,根据勾股定理得到BC=![]() =4,根据圆周角定理得到∠DFC=90°,根据等腰三角形“三线合一”的性质可得BF=
=4,根据圆周角定理得到∠DFC=90°,根据等腰三角形“三线合一”的性质可得BF=![]() BC=2,根据三角函数的定义即可得到结论.
BC=2,根据三角函数的定义即可得到结论.
(1)FG与⊙O相切,
理由:如图,连接OF,
∵∠ACB=90°,D为AB的中点,
∴CD=BD,
∴∠DBC=∠DCB,
∵OF=OC,
∴∠OFC=∠OCF,
∴∠OFC=∠DBC,
∴OF∥DB,
∴∠OFG+∠DGF=180°,
∵FG⊥AB,
∴∠DGF=90°,
∴∠OFG=90°,
∴FG与⊙O相切.
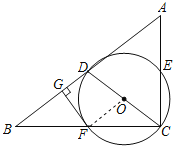
(2)连接DF,
∵CD=2.5,
∴AB=2CD=5,
∵AC=3,
∴BC=![]() =4,
=4,
∵CD为⊙O的直径,
∴∠DFC=90°,
∴FD⊥BC,
∵DB=DC,
∴BF=![]() BC=2,
BC=2,
∵sin∠ABC=![]() ,
,
即![]() ,
,
∴FG=![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
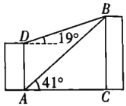
【题目】如图,已知一居民楼![]() 前方
前方![]() 处有一建筑物
处有一建筑物![]() ,小敏在居民楼的顶部
,小敏在居民楼的顶部![]() 处和底部
处和底部![]() 处分别测得建筑物顶部
处分别测得建筑物顶部![]() 的仰角为
的仰角为![]() 和
和![]() ,求居民楼的高度
,求居民楼的高度![]() 和建筑物的高度
和建筑物的高度![]() (结果取整数).
(结果取整数).
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 的顶点分别为 A(-2,2)、B(-4,5)、C(-5,1)和直线 m (直线 m 上各点的横坐标都为 1).
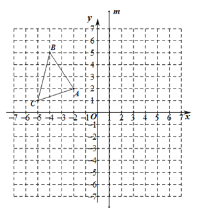
(1)作出△ABC 关于 ![]() 轴对称的图形△A1B1C1,并写出点 A1 的坐标;
轴对称的图形△A1B1C1,并写出点 A1 的坐标;
(2)作出点 C关于直线 m 对称的点C2 , 并写出点C2 的坐标;
(3)在![]() 轴上找一点P,使 PA+PC的值最小,请直接写出点P的坐标.
轴上找一点P,使 PA+PC的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
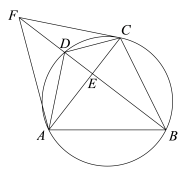
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月饼是中华民族的传统美食,在中秋节期间,小邱家买了三种不同馅的月饼,分别是:肉松月饼(记为![]() ),豆沙月饼(记为
),豆沙月饼(记为![]() ),莲蓉月饼(记为
),莲蓉月饼(记为![]() ).这些月饼除了馅不同,其余均相同.小邱的妈妈在一个盘子中放入了一个肉松月饼,一个豆沙月饼和两个莲蓉月饼.根据以上情况,请你回答下列问题
).这些月饼除了馅不同,其余均相同.小邱的妈妈在一个盘子中放入了一个肉松月饼,一个豆沙月饼和两个莲蓉月饼.根据以上情况,请你回答下列问题
(1)假设小邱从盘子中随机取一个月饼恰好取到肉松月饼概率是多少?
(2)若小邱先从盘子中随机取一个月饼,吃完后再随机取一个,请用列表法或画树状图法求小邱取到的两个月饼中至少有一个是莲蓉月饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() 为
为![]() 内一点,将
内一点,将![]() 绕点
绕点![]() 按逆时针方向旋转角
按逆时针方向旋转角![]() 得到
得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,且
,且![]() 三点在同一直线上.
三点在同一直线上.
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)如图2,若![]() ,请补全图形,再过点
,请补全图形,再过点![]() 作
作![]() 于点
于点![]() ,然后探究线段
,然后探究线段![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)若![]() ,且点
,且点![]() 满足
满足![]() ,直接写出点
,直接写出点![]() 到
到![]() 的距离.
的距离.
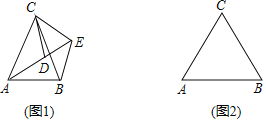
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】皮特是红树林中学的一个外籍教师,目前,他在电脑上打英语单词的平均速度是打汉字速度的2倍.某次,他连续打完一篇3600字(单词)的英语文章和一篇600字的汉语文章,一共刚好花了40分钟.(速度按每分钟打多少个英语单词或汉字测算).
(1)皮特目前平均每分钟打多少汉字;
(2)最近,皮特把一篇汉语文章翻译成英文,原文加上译文总字数为6000字,已知它在1小时内(含1小时)打完了这6000字,问原文最多有多少汉字?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com