
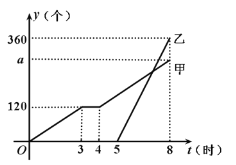
【题目】某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两车间各自加工零件的数量y(个)与甲车间加工时间t(时)之间的函数图象如图所示.
(1)求乙车间加工零件的数量y与甲车间加工时间t之间的函数关系式,并写出t的取值范围.
(2)求甲车间加工零件总量a.
(3)当甲、乙两车间加工零件总数量为320个时,直接写出t的值.
【答案】(1)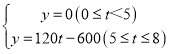 ;(2)280;(3)6
;(2)280;(3)6
【解析】
(1)设y乙与时间t之间的函数关系式为:y=kt+b,结合图像将点(5,0),(8,360)代入求解即可;
(2)根据甲车间前三分种的数据算出甲车间生产效率,从而算出a值;
(3)求出甲车间在4分钟至8分钟内表达式,并和乙车间生产量相加,令和为320,解出t值即可.
解:(1)当0≤t<5时,y乙=0,
当5≤t≤8时,设y乙与时间t之间的函数关系式为:y=kt+b,
将(5,0),(8,360)代入得:![]() ,
,
解得:![]() ,
,
则y乙=120t-600(5≤t≤8),
∴乙车间加工零件的数量y与甲车间加工时间t之间的函数关系式为:
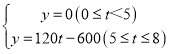 ;
;
(2)∵甲车间的效率不变,在前三分钟内生产了120个,
∴甲车间的效率为每小时120÷3=40(个),
∴甲车间的生产总量为a=120+(8-4)×40=280(个);
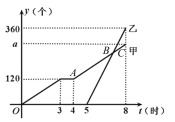
(3)如图, A(4,120),C(8,280),
设AC段的表达式为y甲=mt+n,将A和B代入得:
![]() ,
,
解得:![]() ,
,
∴线段AC的表达式为:y甲=40t-40,
根据题意当t>4时,两车间的总量能达到320个,
∴y甲+ y乙=40t-40+120t-600=320,
解得:t=6.
则此时t的值为6.


科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
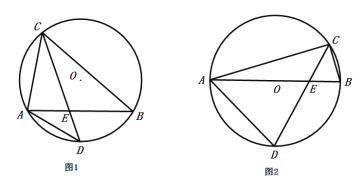
(1)求证:△ADE∽△CDA
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,知道它们都到达点
运动,知道它们都到达点![]() 为止.若
为止.若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则
,则![]() 与
与![]() 的函数图象是( )
的函数图象是( )
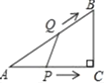
A.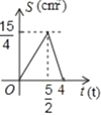 B.
B.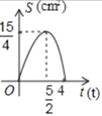 C.
C. D.
D.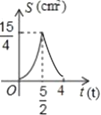
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应香洲区全面推进书香校园建设的号召,班长小青随机调查了若干同学一周课外阅读的时间t(单位:小时),将获得的数据分成四组,绘制了如下统计图(A:0<t≤7,B:7<t≤14,C:14<t≤21,D:t>21),根据图中信息,解答下列问题:
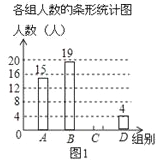
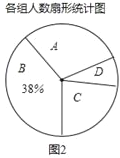
(1)这项工作中被调查的总人数是多少?
(2)补全条形统计图,并求出表示A组的扇形统计图的圆心角的度数;
(3)如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表,请用列表或树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全区范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽部分使用电瓶车的市民,就骑电瓶车戴安全帽情况(![]() :每次戴、
:每次戴、![]() :经常戴、
:经常戴、![]() :偶尔戴、
:偶尔戴、![]() :都不戴)进行问卷调查,将相关的数据制成如下统计图表.
:都不戴)进行问卷调查,将相关的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
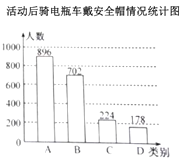
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该区约有37万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,谈谈你对交警部门宣传活动的效果的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
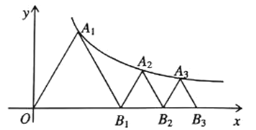
【题目】如图,已知等边三角形![]() ,顶点
,顶点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 的坐标为
的坐标为![]() .过
.过![]() 作
作![]() 交双曲线于点
交双曲线于点![]() ,过
,过![]() 作
作![]()
![]() 交
交![]() 轴于点
轴于点![]() ,得到第二个等边
,得到第二个等边![]() ;过
;过![]() 作
作![]() 交双曲线于点
交双曲线于点![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,得到第三个等边
,得到第三个等边![]() ;以此类推,... 则点
;以此类推,... 则点![]() 的坐标为____.
的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
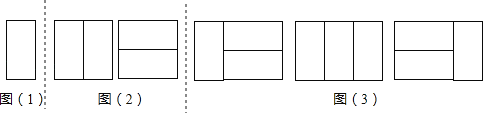
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
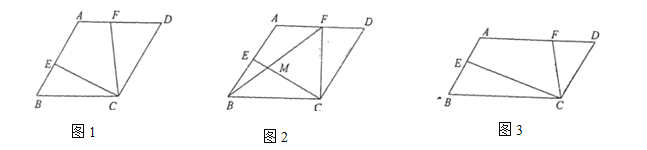
(2)如图2,若![]() ,且点
,且点![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,求
,求![]() ;
;
(3)如图3,若![]() ,探究线段
,探究线段![]() 、
、![]() 、
、![]() 三之间的数量关系,说明理由.
三之间的数量关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
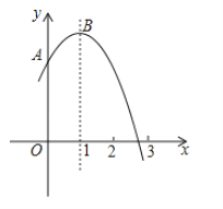
【题目】如图,抛物线![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,顶点为
之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]()
③将该抛物线向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得抛物线解析式为
个单位,所得抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() 点
点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中正确判断的序号是( )
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com