
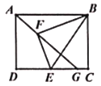
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
A.1B.1.5C.4-![]() D.4-
D.4-![]()
【答案】D
【解析】
由图可知:DG最小时CG最大,故当∠GAD最小(∠GAB最大)时,CG取最大值,由F在以B为圆心,BC为半径的圆上得到AF⊥BF,此时点G、E重合,证明△ABF≌△AED,得到AE=AB=4,再利用勾股定理求出DE即可得到CG的最大值.
由图可知:DG最小时CG最大,故当∠GAD最小(∠GAB最大)时,CG取最大值,
∵F在以B为圆心,BC为半径的圆上,
∴AF与圆相切时,∠GAB最大,
即AF⊥BF,此时点G、E重合,
∵AB∥CD,
∴∠BAF=∠AED,
∵∠AFB=∠D=90°,BF=BC=AD,
∴△ABF≌△AED,
∴AE=AB=4,
∴DE=![]() ,
,
∴CE=CG=![]() ,
,
故选:D.


科目:初中数学 来源: 题型:
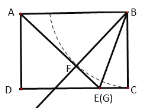
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
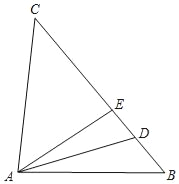
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国诗词大会”带着我们“赏中华诗词、寻文化基因、品生活之美”,从古人的智慧和情怀中汲取营养、涵养心灵,其中的“飞花令”环节,在广大青少年中圈粉无数.西安铁一中分校初三二班的同学们准备在班内举行“飞花令”比赛,组织过程如下:全班同学分成五个小组,每个小组派5名同学参加比赛,这5名同学依次从写有“春”、“云”、“月”、“花”、“夜”的五张卡片中随机摸出一张(不放回),5个小组中抽取相同字的同学进行比赛(例如5名抽到“春”字同学进行以“春”为主题字的飞花令比赛).第一小组的小丽和第二小组的小英分别是各自小组第一个抽取卡片的同学.
(1)求小丽抽到“春”的概率;
(2)小丽和小英都比较擅长“春”和“月”为主题的诗句,求她们至少有一人抽到自己擅长的主题字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
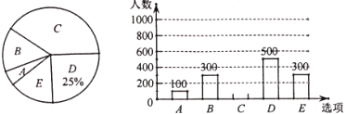
(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 ;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A,B,C三种交通工具中随机选择一种,乙上班时从B、C、D三种交通工具中随机选择一种,请用树状图法或列表法求甲、乙两人都不选B种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( )
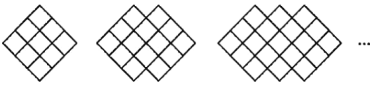
A.400B.401C.402D.403
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在10盒红色的笔芯中混放了若干支黑色的笔芯,每盒20支笔芯,每盒中混放入的黑色笔芯数如下表:
黑色笔芯数 | 0 | 1 | 4 | 5 | 6 |
盒数 | 2 | 4 | 1 | 2 | 1 |
下列结论:
①黑色笔芯一共有16支;
②从中随机取一盒,盒中红色笔芯数不低于14是必然事件;
③从中随机取一盒,盒中黑色笔芯数不超过4的概率为0.7;
④将10盒笔芯混在一起,从中随机抽取一支笔芯,恰好是黑色的概率是0.12.
其中正确的结论有()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十三五”以来,山西省共解决372个村、35.8万农村人口的饮水型氟超标问题,让农村群众真正喝上干净水、放心水、安全水.某公司抓住商机,根据市场需求代理![]() ,
,![]() 两种型号的净水器,已知每台
两种型号的净水器,已知每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型,
型,![]() 型净水器的进价各是多少元?
型净水器的进价各是多少元?
(2)该公司计划购进![]() ,
,![]() 两种型号的净水器共55台进行试销,其中
两种型号的净水器共55台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买两种净水器的总资金不超过10.8万元.则最多可购进
台,购买两种净水器的总资金不超过10.8万元.则最多可购进![]() 型号净水器多少台?
型号净水器多少台?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com