
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
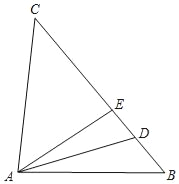
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
【答案】(1)证明见解析(2)48°
【解析】
(1)根据等腰三角形的性质得到∠CAD=∠CDA,根据角平分线的定义得到∠EAD=∠BAD,于是得到结论;
(2)设∠DAB=x,得到∠C=3x,根据角平分线的定义得到∠EAB=2∠DAB=2x,求得∠CAB=∠CAE+∠EAB=50°+2x,根据三角形的内角和即可得到结论.
(1)∵CA=CD,
∴∠CAD=∠CDA,
∵AD平分∠BAE,
∴∠EAD=∠BAD,
∵∠B=∠CDA﹣∠BAD,∠CAE=∠CAD﹣∠DAE,
∴∠CAE=∠B;
(2)设∠DAB=x,
∵∠C=∠3∠DAB,
∴∠C=3x,
∵∠CAE=∠B,∠B=50°,
∴∠CAE=50°,
∵AD平分∠BAE,
∴∠EAB=2∠DAB=2x,
∴∠CAB=∠CAE+∠EAB=50°+2x,
∵∠CAB+∠B+∠C=180°,
∴50°+2x+50°+3x=180°,
∴x=16°,
∴∠C=3×16°=48°.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A
(a>0,b<0)的图象与x轴只有一个公共点A
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月1日,中华人民共和国70年华诞之际,王梓涵和学校国旗护卫队的其他同学们赶到学校举行了简朴而降重的升旗仪式.倾听着雄壮的国歌声,目送着五星红旗级缓升起,不禁心潮澎湃,爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高度.将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端2米,然后将绳子末端拉直到距离旗杆5m处,测得此时绳子末端距离地面高度为1m,最后根据刚刚学习的勾股定理就能算出旗杆的高度为( )
A.10mB.11mC.12mD.13m
查看答案和解析>>
科目:初中数学 来源: 题型:
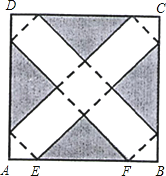
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A.B.C.D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形, D、 E分别在边AB、AC上,且AD=CE,CD与BE相交于点O.
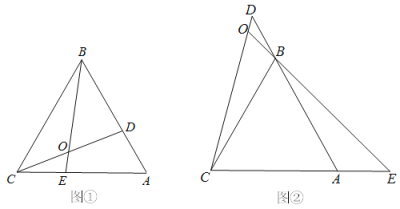
(1)如图①,求∠BOD的度数;
(2)如图②,如果点D、 E分别在边AB、CA的延长线上时,且AD=CE,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
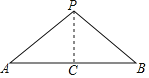
【题目】已知,如图,点![]() 在线段
在线段![]() 外,且
外,且![]() ,求证:点
,求证:点![]() 在线段
在线段![]() 的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
A.作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() B.过点
B.过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C.取![]() 中点
中点![]() ,连接
,连接![]() D.过点
D.过点![]() 作
作![]() ,垂足为
,垂足为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毎年6月,学校门口的文具店都会购进毕业季畅销商品进行销售.已知校门口“小光文具店“在5月份就售出每本8元的A种品牌同学录90本,每本10元的B种品牌同学录175本.
(1)某班班长帮班上同学代买A种品牌和B种品牌同学录共27本,共花费246元,请问班长代买A种品牌和B种品牌同学录各多少本?
(2)该文具店在6月份决定将A种品牌同学录每本降价3元后销售,B种品牌同学录每本降价a%(a>0)后销售.于是,6月份该文具店A种品牌同学录的销量比5月份多了![]() a%,B种品牌同学录的销量比5月份多了(a+20)%,且6月份A、B两种品牌的同学录的销售总额达到了2550元,求a的值.
a%,B种品牌同学录的销量比5月份多了(a+20)%,且6月份A、B两种品牌的同学录的销售总额达到了2550元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com