
����Ŀ��ij��˾����һ�ֳɱ�����Ϊ50Ԫ/�����²�Ʒ���涨����ʱ���۵��۲����ڳɱ����ۣ��ֲ�����80Ԫ/�������������飬����������y�����������۵���x��Ԫ/�����ɽ��ƿ���һ�κ���y��kx+b�Ĺ�ϵ����ͼ��ʾ��
��I������ͼ����һ�κ���y��kx+b�Ľ���ʽ����д���Ա���x��ȡֵ��Χ��
���ù�˾Ҫ��ÿ������������Ӧ�����۵��۶�Ϊ���٣��������ֵΪ���٣�

���𰸡���1��y=��x+100��50��x��80������2�����۵��۶�Ϊ75Ԫ/�����������Ϊ625Ԫ��
��������
��1���������⣬���ô���ϵ������һ�κ����Ľ���ʽ��������2����ÿ���õ�����ΪWԪ����������W�����۵���x�Ķ��κ���ģ�ͣ����ݶ��κ��������ʼ��������
�⣺��1���ɺ�����ͼ��ã�![]() ��
��
��ã�![]() ��
��
������y=��x+100��50��x��80����
��2����ÿ���õ�����ΪWԪ��
����1���ã�W=��x��50��y=��x��50������x+100��=��x2+150x��5000=����x��75��2+625��
����1��0��
�൱x=75ʱ��W���=625���ù�˾Ҫ��������������Ӧ�����۵���Ϊ75Ԫ/�����������Ϊ625Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��EΪBC�ϵĵ㣬ADƽ�֡�BAE��CA=CD��
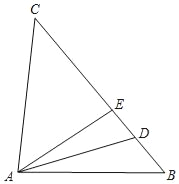
��1����֤����CAE����B��
��2������B��50�㣬��C��3��DAB�����C�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�ij����Ʒƽ��ÿ�������30����ÿ��ӯ��50Ԫ��Ϊ�˾�����ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣�ÿ����Ʒÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2������ÿ����Ʒ����![]() Ԫ���ݴ˹��ɣ���ش�
Ԫ���ݴ˹��ɣ���ش�
��1���̳�������������_____����ÿ����Ʒӯ��_____Ԫ���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���������������䡢������������£�ÿ����Ʒ���۶���Ԫʱ���̳���ӯ���ɴﵽ2100Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У�
��![]() ��
��![]() ����һ�㣬
����һ�㣬
��1����![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת��ʹ
��˳ʱ�뷽����ת��ʹ![]() ��
��![]() �غϣ��õ�
�غϣ��õ�![]() ����ͼ��a����ʾ���۲��֪����
����ͼ��a����ʾ���۲��֪����![]() ��ȵ��߶���__________��
��ȵ��߶���__________��![]() __________��
__________��
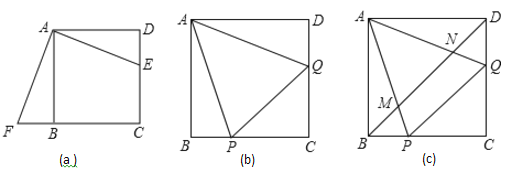
��2����ͼ��b����ʾ��������![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���ϵĵ㣬��
���ϵĵ㣬��![]() ����ͨ����ת�ķ�ʽ˵����
����ͨ����ת�ķ�ʽ˵����![]() ��
��
��3���ڣ�2���������£�����![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����ͼ��c����ʾ���ж�
����ͼ��c����ʾ���ж�![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ��ֱ��д�����ۣ�
֮��Ĺ�ϵ��ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߶�AB�������˵�����ֱ�Ϊ����2��1���ͣ�2��3����
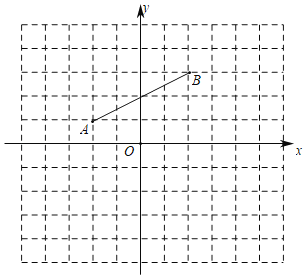
��1����ͼ�зֱ��߶�AB����x��ĶԳ��߶�A1B1����д��A1��B1�����꣮
��2����x������һ��C��ʹAC+BC��ֵ��С����ͼ��������C����ֱ��д����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ù���ȫ��������������������У���һ�ֵ��͵����ñ������ߵķ��������磺����ABC�У�AB��8��AC��6����D��BC���ϵ��е㣬������AD��ȡֵ��Χ�أ����ǿ����ӳ�AD����E��ʹAD��DE��Ȼ������BE����ͼ�٣�������������ADC����EDB�У�����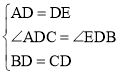 �����ADC�ա�EDB����AC��EB��������������ABE��ͨ��AE�ij������AD��ȡֵ��Χ��
�����ADC�ա�EDB����AC��EB��������������ABE��ͨ��AE�ij������AD��ȡֵ��Χ��
����ش�
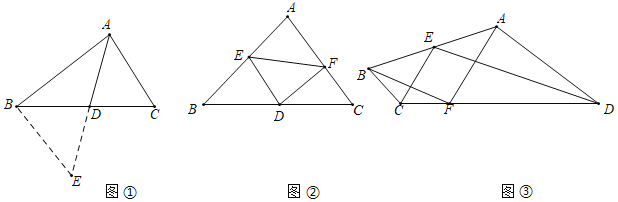
��1����ͼ���У�����AD��ȡֵ��Χ���� ����
��2��Ӧ�����������������������
����ͼ�ڣ�����ABC�У���D��BC���ϵ��е㣬��E��AB���ϵ�һ�㣬��DF��DE��AC���ڵ�F������EF����BE��4��CF��2����ֱ��д��EF��ȡֵ��Χ��
����ͼ�ۣ����ı���ABCD�У���BCD��150������ADC��30������E��AB�е㣬��F��DC�ϣ�������BC��CF��DF��AD������CE��ED�����ж�CE��ED��λ�ù�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����BAC��48������BAC��ƽ�������߶�AB�Ĵ�ֱƽ����OD���ڵ�O������OB��OC������ACB��EF��E��BC�ϣ�F��AC�ϣ��۵�����C���Oǡ���غϣ����OECΪ_____�ȣ�
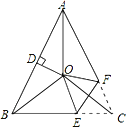
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ�����O����BAD=120�㣬ACƽ����BAD��AC��BD�ཻ��E�㣬���н��۴�����ǣ�������
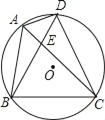
A. ��BDCΪ�ȱ������� B. ��AED=��ABC
C. ��ABE�ס�DBA D. BC2=CECA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������ij�������ۺ�����ָ�Ӳ���������![]() ��
��![]() �����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����
�����ͺŵ���ˮ�����豸��10̨����֪��90��Ԫ����![]() �ͺŵ���ˮ�����豸��̨������75��Ԫ����
�ͺŵ���ˮ�����豸��̨������75��Ԫ����![]() �ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
�ͺŵ���ˮ�����豸��̨����ͬ��ÿ̨�豸�۸��´�����ˮ�����±���ʾ��
��ˮ�����豸 |
|
|
�۸���Ԫ/̨�� |
|
|
�´�����ˮ������/̨�� | 220 | 180 |
��1����![]() ��ֵ��
��ֵ��
��2���������ʽ����ƣ�ָ�Ӳ����ڹ�����ˮ�����豸���ʽ���156��Ԫ�����ж����ֹ����������ÿ����ദ����ˮ���Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com