
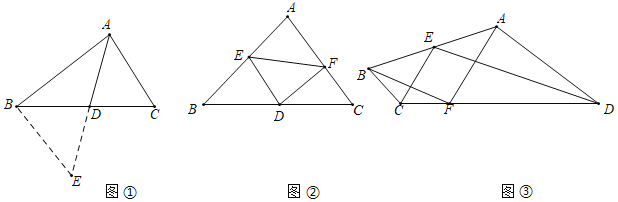
【题目】在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB=8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于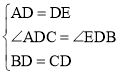 ,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
请你回答:
(1)在图①中,中线AD的取值范围是 .
(2)应用上述方法,解决下面问题
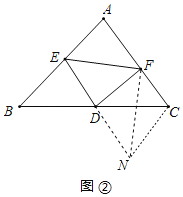
①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.
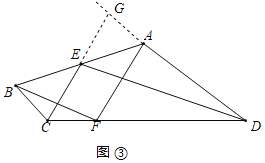
②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.
【答案】(1)1<AD<7;(2)①2<EF<6;②CE⊥ED,理由见解析
【解析】
(1)在△ABE中,根据三角形的三边关系定理即可得出结果;
(2)①延长ED到点N,使![]() ,连接CN、FN,由SAS证得
,连接CN、FN,由SAS证得![]() ,得出
,得出![]() ,由等腰三角形的性质得出
,由等腰三角形的性质得出![]() ,在△CFN中,根据三角形的三边关系定理即可得出结果;
,在△CFN中,根据三角形的三边关系定理即可得出结果;
②延长CE与DA的延长线交于点G,易证DG∥BC,得出![]() ,由ASA证得
,由ASA证得![]() ,得出
,得出![]() ,即可证得
,即可证得![]() ,由
,由![]() ,根据等腰三角形的性质可得出
,根据等腰三角形的性质可得出![]() .
.
(1)在△ABE中,由三角形的三边关系定理得:![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
故答案为:![]() ;
;
(2)①如图②,延长ED到点N,使![]() ,连接CN、FN
,连接CN、FN
∵点D是BC边上的中点
![]()
在△NDC和△EDB中,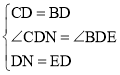
![]()
![]()
![]()
![]() 是等腰三角形,
是等腰三角形,![]()
在△CFN中,由三角形的三边关系定理得:![]()
![]() ,即
,即![]()
![]() ;
;
②![]() ;理由如下:
;理由如下:
如图③,延长CE与DA的延长线交于点G
∵点E是AB中点
![]()
![]()
![]()
![]()
在△GAE和△CBE中,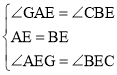
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]() .(等腰三角形的三线合一)
.(等腰三角形的三线合一)


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形, D、 E分别在边AB、AC上,且AD=CE,CD与BE相交于点O.
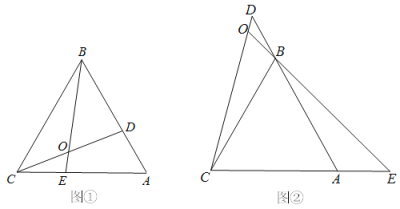
(1)如图①,求∠BOD的度数;
(2)如图②,如果点D、 E分别在边AB、CA的延长线上时,且AD=CE,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
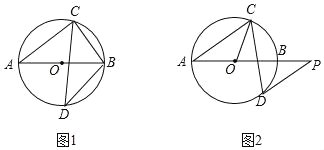
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=40°.
(1)如图1,若D为弧AB的中点,求∠ABC和∠ABD的度数;
(2)如图2,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
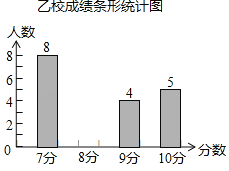
【题目】甲、乙两校参加学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分),乙校平均分是8.3分,乙校的中位数是8分.依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图;
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | ■ | 8 |
(1)请你将乙校成绩统计图直接补充完整;
(2)请直接写出甲校的平均分是 ,甲校的中位数是 ,甲校的众数是 ,从平均分和中位数的角度分析 校成绩较好(填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
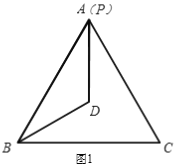
【题目】已知△ABC是等边三角形,P为△ABC所在平面内一个动点,BP=BA,若0°﹤∠PBC﹤ 180°,且∠PBC的平分线上一点D满足DB=DA.
(1)当BP和BA重合时(如图1),则∠BPD=______°.
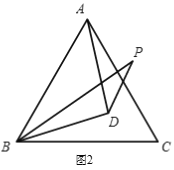
(2)当BP在∠ABC内部时(如图2),求∠BPD的度数
(3)当BP在∠ABC外部时,请直接写出∠BPD的度数,并画出相应的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )
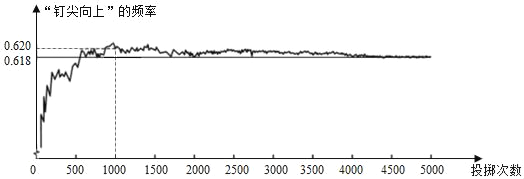
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com