
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=40°.
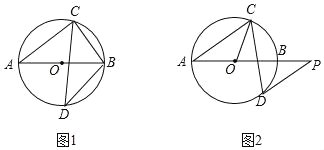
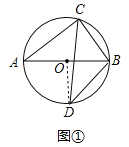
(1)如图1,若D为弧AB的中点,求∠ABC和∠ABD的度数;
(2)如图2,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数.
【答案】(1)45°;(2)26°.
【解析】
(1)根据圆周角和圆心角的关系和图形可以求得∠ABC和∠ABD的大小;
(2)根据题意和平行线的性质、切线的性质可以求得∠OCD的大小.
(1)∵AB是⊙O的直径,∠BAC=38°, ∴∠ACB=90°,
∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°,
∵D为弧AB的中点,∠AOB=180°,∴∠AOD=90°,
∴∠ABD=45°;
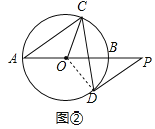
(2)连接OD,
∵DP切⊙O于点D,∴OD⊥DP,即∠ODP=90°,
∵DP∥AC,∠BAC=38°,∴∠P=∠BAC=38°,
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,∴∠ACD=64°,
∵OC=OA,∠BAC=38°,∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
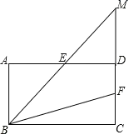
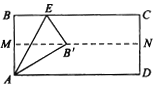
【题目】如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
(1)求证:四边形ABCD为矩形;
(2)若MD=6,BC=12,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若![]() ,则折痕AE的长为( )
,则折痕AE的长为( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB=8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于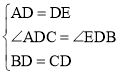 ,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
请你回答:
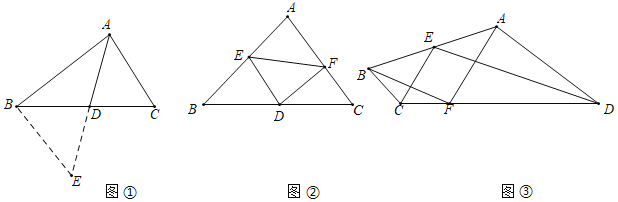
(1)在图①中,中线AD的取值范围是 .
(2)应用上述方法,解决下面问题
①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.
②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种原料,运往A地和B地销售.如表记录的是该产品运往A地和B地供应量y1(kg)、y2(kg)与销售价格x(元)之间的关系:
销售价格x(元) | 100 | 150 | 200 | 300 |
运往A地y1(kg) | 300 | 250 | 200 | 100 |
运往B地y2(kg) | 450 | 350 | 250 | n |
(1)请认真分析上表中所给数据,用你所学过的函数来表示其变化规律,并验证你的猜想,分别求出y1与x、y2与x的函数关系式;
(2)用你求出的函数关系式完成上表,直接写出n= ;
(3)直接写出销售价格在 元时,该产品运往A地的供应量等于运往B地的供应量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库有50件同一规格的某种集装箱,准备委托运输公司送到码头,运输公司有每次可装运1件、2件、3件这种集装箱的三种型号的货车,这三种型号的货车每次收费分别为120元、160元、180元现要求安排20辆货车刚好一次装运完这些集装箱,问这三种型号的货车各需多少辆?有多少种安排方式?哪些安排方式所需的运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
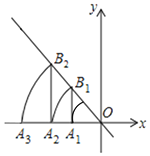
【题目】如图,直线![]() :
:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 轴负半轴于点
轴负半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 轴负半轴于点
轴负半轴于点![]() ;…,按此作法进行下去.点
;…,按此作法进行下去.点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
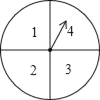
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com