
【题目】如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若![]() ,则折痕AE的长为( )
,则折痕AE的长为( )
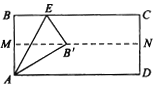
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD,下列结论:①EG⊥FH;②四边形EFGH是菱形;③HF平分∠EHG;④EG=![]() (BC﹣AD),其中正确的个数是( )
(BC﹣AD),其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
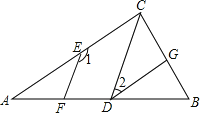
【题目】已知:如图EF∥CD,∠1+∠2=180°.
(1)试说明GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏思考解决如下问题:
原题:如图1,点![]() ,
,![]() 分别在菱形
分别在菱形![]() 的边
的边![]() ,
,![]() 上,
上,![]() ,求证:
,求证:![]() .
.
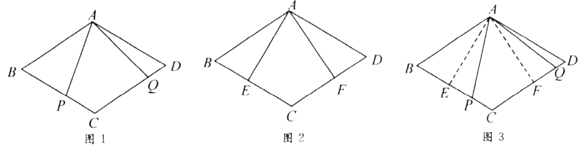
(1)小敏进行探索,若将点![]() ,
,![]() 的位置特殊化:把
的位置特殊化:把![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,使
,使![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,如图2,此时她证明了
上,如图2,此时她证明了![]() .请你证明.
.请你证明.
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .请你继续完成原题的证明.
.请你继续完成原题的证明.
(3)如果在原题中添加条件:![]() ,
,![]() ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
查看答案和解析>>
科目:初中数学 来源: 题型:
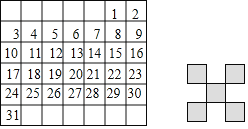
【题目】如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“![]() ”形中的5个数字的最小数为a.
”形中的5个数字的最小数为a.
![]() 请用含a的代数式表示这5个数;
请用含a的代数式表示这5个数;
![]() 这五个数的和与“
这五个数的和与“![]() ”形中心的数有什么关系?
”形中心的数有什么关系?
![]() 盖住的5个数字的和能为105吗?为什么?
盖住的5个数字的和能为105吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动) .
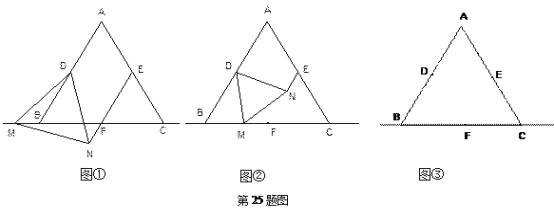
(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?点F是否在直线NE上?都请直接写出结论,不必证明或说明理由;
(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图②证明;若不成立,请说明理由;
(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论,不必证明或说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com