
����Ŀ��ij��˾����һ��ԭ�ϣ�����A�غ�B�����ۣ������¼���Ǹò�Ʒ����A�غ�B�ع�Ӧ��y1��kg����y2��kg�������ۼ۸�x��Ԫ��֮��Ĺ�ϵ��
���ۼ۸�x��Ԫ�� | 100 | 150 | 200 | 300 |
����A��y1��kg�� | 300 | 250 | 200 | 100 |
����B��y2��kg�� | 450 | 350 | 250 | n |
��1������������ϱ����������ݣ�������ѧ���ĺ�������ʾ��仯���ɣ�����֤��IJ��룬�ֱ����y1��x��y2��x�ĺ�����ϵʽ��
��2����������ĺ�����ϵʽ����ϱ���ֱ��д��n���� ����
��3��ֱ��д�����ۼ۸����� ��Ԫʱ���ò�Ʒ����A�صĹ�Ӧ����������B�صĹ�Ӧ����
���𰸡���1��y1����x+400��y2����2x+650����2��50����3��250
��������
��1��ͨ���۲췢�֣�y1��y2����x��һ�κ��������ô���ϵ�������ɽ����
��2�����ã�1���Ľ�����![]() ,�����
,�����![]() ֵ��Ϊn��ֵ��
ֵ��Ϊn��ֵ��
��3�����ݣ�1���Ľ��ۣ���![]() ���з��̽�ɣ�
���з��̽�ɣ�
�⣺��1����y1��x�ĺ�����ϵʽΪy1��k1x+b1������������
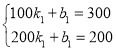 ���
���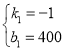
��y1����x+400��
��֤����![]() ʱ��
ʱ��![]() �� ��
�� ��![]() ʱ��
ʱ��![]()
��y2��x�ĺ�����ϵʽΪy2��k2x+b2��
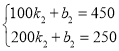 ���
���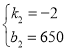
��y2����2x+650��
��֤����![]() ʱ��
ʱ��![]() ��
��
��2����x��300ʱ��n=y2����2x+650����2��300+650��50��
�ʴ�Ϊ��50��
��3������������x+400����2x+650��
���x��250��
�����ۼ۸���250Ԫʱ���ò�Ʒ����A�صĹ�Ӧ����������B�صĹ�Ӧ����
�ʴ�Ϊ��250��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
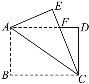
����Ŀ����ͼ���ھ���ֽƬABCD�У�AB��4��BC��6������ABC��AC�۵���ʹ��B���ڵ�E����CE��AD�ڵ�F����DF�ij�����(����)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��(m��1)x��2m2��m=0��mΪʵ����������ʵ����x1��x2��
��1����mΪ��ֵʱ��x1=x2.
��2����x12+x22����m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ABC��90�㣬AB��BC��ֱ��l1��l2��l3�ֱ�ͨ��A��B��C���㣬��l1��l2��l3����l1��l2�ľ���Ϊ5��l2��l3�ľ���Ϊ7����Rt��ABC�����Ϊ___________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
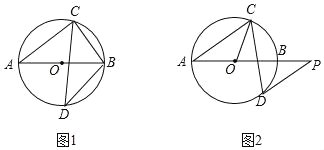
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB�ཻ����BAC��40�㣮
��1����ͼ1����DΪ��AB���е㣬���ABC�͡�ABD�Ķ�����
��2����ͼ2������D����O�����ߣ���AB���ӳ��߽��ڵ�P����DP��AC�����OCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������A��
������A��![]() ��0����B��
��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE����AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�������·��ͨ�����������涨��С�����ڳǽ�·����ʻ�ٶȲ��ó���![]() km/h.��ͼ��һ��С������һ�����н�·��ֱ����ʻ��ijһʱ�̸պ���ʻ��·���泵�ټ������ǰ��
km/h.��ͼ��һ��С������һ�����н�·��ֱ����ʻ��ijһʱ�̸պ���ʻ��·���泵�ټ������ǰ��![]() m��������2s���С�����복�ټ���Ǽ����Ϊ
m��������2s���С�����복�ټ���Ǽ����Ϊ![]() m������С������������
m������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
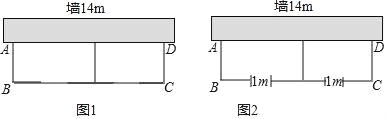
����Ŀ����ͼ���г�Ϊ22����ʣ�һ������ǽ��ǽ�������ó���Ϊ14�ף���Χ���м����һ����ʵij����λ��ԣ�����������Χ����
��1����ͼ1���軨�ԵĿ�ABΪx�ף����Ϊy��2����y��x֮��ĺ���������ʽ����ȷ��x��ȡֵ��Χ��
��2����ͼ2��Ϊ�˷�����룬�ڽ�����ʻ���ʱ����BC���������������˿�Ϊ1������С�ţ��軨�ԵĿ�ABΪa�ף����ΪS��2����S��a֮��ĺ�������ʽ��S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
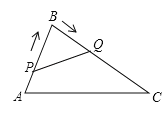
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AB��8cm��BC��16 cm.��P�ӵ�A������AB���B��2 cm/s���ٶ��˶�����Q�ӵ�B������BC���C��4 cm/s���ٶ��˶��������P��Q�ֱ�ӵ�A��Bͬʱ��������_____________���Ӻ��PBQ���ABC���ƣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com