
【题目】如图,已知△ABC是等边三角形, D、 E分别在边AB、AC上,且AD=CE,CD与BE相交于点O.
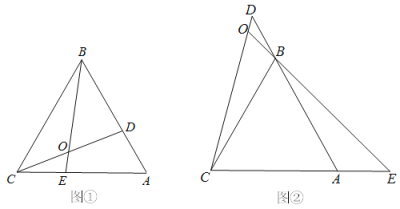
(1)如图①,求∠BOD的度数;
(2)如图②,如果点D、 E分别在边AB、CA的延长线上时,且AD=CE,求∠BOD的度数.
【答案】(1)∠BOD=60°;(2)∠BOD=120°.
【解析】
(1)根据等边三角形的性质可得BC=AC, ∠BCE=∠CAD =60°,然后利用SAS即可证出△BCE≌△CAD,从而得出∠CBE=∠ACD,然后利用等量代换和三角形外角的性质即可求出∠BOD的度数;
(2)根据等边三角形的性质可得BC=AC, ∠BCE=∠CAD =60°,然后利用SAS即可证出△BCE≌△CAD,从而得出∠CBE=∠ACD,然后利用三角形内角和定理、等量代换和三角形外角的性质即可求出∠BOD的度数.
解:(1)∵△ABC是等边三角形
∴BC=AC, ∠BCE=∠CAD =60°
在△BCE与△CAD中
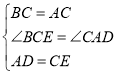
∴△BCE≌△CAD.
∴∠CBE=∠ACD.
∵∠BCD+∠ACD=60°
∴∠BCD+∠CBE=60°
又∵∠BOD=∠BCD+∠CBE
∴∠BOD=60°
(2)∵△ABC是等边三角形
∴BC=AC,∠BCE=∠CAD =60°
在在△BCE与△CAD中
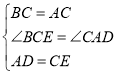
∴△BCE≌△CAD
∴∠CBE=∠ACD
而∠CBE+∠BCA+∠E=180°,∠BCA=60°
∴∠ACD+60°+∠E=180°
∴∠ACD+∠E=120°
又∵∠BOD=∠ACD+∠E
∴∠BOD=120°.


科目:初中数学 来源: 题型:
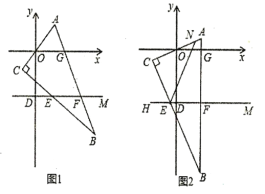
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 平行于
平行于![]() 轴并交
轴并交![]() 轴于
轴于![]() ,一块三角板摆放其中,其边与
,一块三角板摆放其中,其边与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 分别交于
分别交于![]() ,
,![]() 两点,
两点,
(1)将三角板如图1所示的位置摆放,请写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(2)将三角板按如图2所示的位置摆放,![]() 为
为![]() 上一点,
上一点,![]() ,请写出
,请写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以M(0,2)圆心,4为半径的⊙M交x轴于A、B两点,交y轴于C、D两点,连结BM并延长交⊙M于点P,连结PC交x轴于点E.
(1)求∠DMP的度数;
(2)求△BPE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
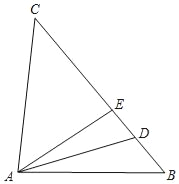
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
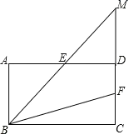
【题目】如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
(1)求证:四边形ABCD为矩形;
(2)若MD=6,BC=12,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
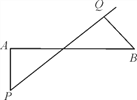
【题目】如图,B地在A地的正东方向,两地相距28![]() km.A,B两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处,至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110 km/h.问:该车是否超速行驶?
km.A,B两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距离相等.上午8:00测得一辆在高速公路上行驶的汽车位于A地的正南方向P处,至上午8:20,B地发现该车在它的西北方向Q处,该段高速公路限速为110 km/h.问:该车是否超速行驶?
查看答案和解析>>
科目:初中数学 来源: 题型:
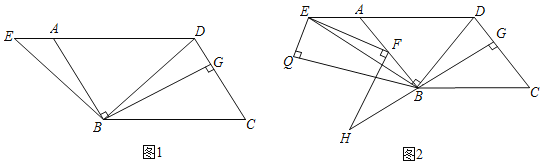
【题目】在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.
(1)如图1,若∠C=60°,∠BDC=75°,BD=6![]() ,求AE的长度;
,求AE的长度;
(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB=8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于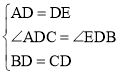 ,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
请你回答:
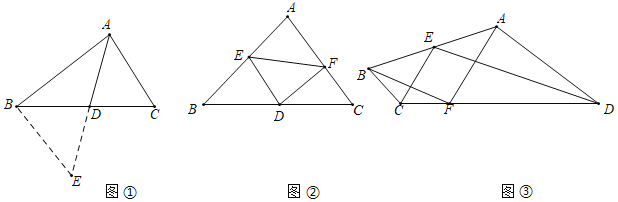
(1)在图①中,中线AD的取值范围是 .
(2)应用上述方法,解决下面问题
①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.
②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com