
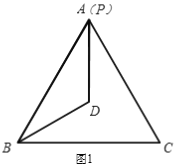
【题目】已知△ABC是等边三角形,P为△ABC所在平面内一个动点,BP=BA,若0°﹤∠PBC﹤ 180°,且∠PBC的平分线上一点D满足DB=DA.
(1)当BP和BA重合时(如图1),则∠BPD=______°.
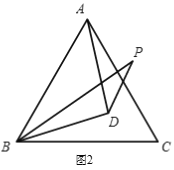
(2)当BP在∠ABC内部时(如图2),求∠BPD的度数
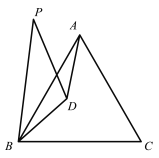
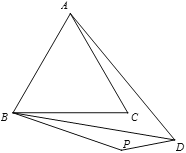
(3)当BP在∠ABC外部时,请直接写出∠BPD的度数,并画出相应的图形.
【答案】(1)30;(2)∠BPD=30°;(3)图形见解析,∠BPD=30°或150°.
【解析】
(1)由于P,A重合,DP=DB,∠DBP=∠DPB,因为DB是∠PBC的平分线,因此,∠DBP=∠DPB=30°;
(2)本题可通过构建全等三角形来求解.连接CD,BP=BC,BD又是∠PBC的平分线,三角形PBD和三角形CBD中又有一公共边,因此两三角形全等,∠BPD=∠BCD,那么关键是求∠BCD的值,那么我们就要看∠BCD和∠ACB的关系了,可通过证明三角形ACD和BCD全等来得出,这两个三角形中,BD=AD,BC=AC,有一条公共边CD因此∠BCD=∠ACD=30°,那么就求出∠BPD的度数了;
(3)同(2)的证法完全一样,步骤有2个,一是得出∠BCD的度数,二是证明三角形BPD和BCD全等,同(2)完全一样.
(当∠BPD是钝角时,∠BPD=∠BCD=(360-60)÷2=150°,还是用的(2)中的三角形BPD,BCD全等,BCD,ACD全等)
解:(1)30°
(2)连结CD
∵ D在∠PBC的平分线上
∴∠PBD=∠CBD
∵△ABC是等边三角形
∴BA=BC=AC,∠ACB=60°
∵BP=BA
∴BP=BC
∵BD=BD
∴△PBD≌△CBD(SAS)
∴∠BPD=∠BCD
∵DB=DA,BC=AC,CD=CD
∴△BCD≌△ACD
∴∠BCD=∠ACD=![]() ∠ACB=30°
∠ACB=30°
∴∠BPD=30°

(3)∠BPD=30°或150°



科目:初中数学 来源: 题型:
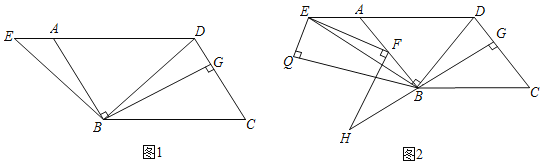
【题目】在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.
(1)如图1,若∠C=60°,∠BDC=75°,BD=6![]() ,求AE的长度;
,求AE的长度;
(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用构造全等三角形来解决的问题中,有一种典型的利用倍延中线的方法,例如:在△ABC中,AB=8,AC=6,点D是BC边上的中点,怎样求AD的取值范围呢?我们可以延长AD到点E,使AD=DE,然后连接BE(如图①),这样,在△ADC和△EDB中,由于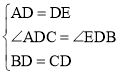 ,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
,∴△ADC≌△EDB,∴AC=EB,接下来,在△ABE中通过AE的长可求出AD的取值范围.
请你回答:
(1)在图①中,中线AD的取值范围是 .
(2)应用上述方法,解决下面问题
①如图②,在△ABC中,点D是BC边上的中点,点E是AB边上的一点,作DF⊥DE交AC边于点F,连接EF,若BE=4,CF=2,请直接写出EF的取值范围.
②如图③,在四边形ABCD中,∠BCD=150°,∠ADC=30°,点E是AB中点,点F在DC上,且满足BC=CF,DF=AD,连接CE、ED,请判断CE与ED的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库有50件同一规格的某种集装箱,准备委托运输公司送到码头,运输公司有每次可装运1件、2件、3件这种集装箱的三种型号的货车,这三种型号的货车每次收费分别为120元、160元、180元现要求安排20辆货车刚好一次装运完这些集装箱,问这三种型号的货车各需多少辆?有多少种安排方式?哪些安排方式所需的运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=120°,AC平分∠BAD,AC与BD相交于E点,下列结论错误的是( )
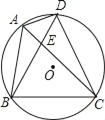
A. △BDC为等边三角形 B. ∠AED=∠ABC
C. △ABE∽△DBA D. BC2=CECA
查看答案和解析>>
科目:初中数学 来源: 题型:
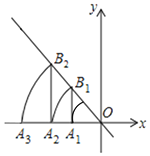
【题目】如图,直线![]() :
:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 轴负半轴于点
轴负半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 轴负半轴于点
轴负半轴于点![]() ;…,按此作法进行下去.点
;…,按此作法进行下去.点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路旁有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() 米,与公路上另一停靠站
米,与公路上另一停靠站![]() 的距离为
的距离为![]() 米,且
米,且![]() ,如图,为了安全起见,爆破点
,如图,为了安全起见,爆破点![]() 周围半径
周围半径![]() 米范围内不得进入,问在进行爆破时,公路
米范围内不得进入,问在进行爆破时,公路![]() 段是否有危险,是否需要暂时封锁?请通过计算进行说明.
段是否有危险,是否需要暂时封锁?请通过计算进行说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE=___________,∠BDE=_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com