
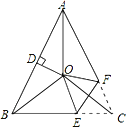
【题目】如图,△ABC中,AB=AC,∠BAC=48°,∠BAC的平分线与线段AB的垂直平分线OD交于点O.连接OB、OC,将∠ACB沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
【答案】96
【解析】
根据角平分线的定义求出∠BAO,根据等腰三角形的性质、三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到OA=OB,得到∠ABO=∠BAO,证明△AOB≌△AOC,根据全等三角形的性质、折叠的性质、三角形内角和定理计算,得到答案.
解:∵∠BAC=48°,AO为∠BAC的平分线,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×48°=24°,
×48°=24°,
∵AB=AC,
∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣48°)=66°,
(180°﹣48°)=66°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=24°,
∴∠OBC=∠ABC﹣∠ABO=66°﹣24°=42°,
在△AOB和△AOC中,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴∠OCB=∠OBC=42°,
由折叠的性质可知,OE=CE,
∴∠COE=∠OCB=42°,
在△OCE中,∠OEC=180°﹣∠COE﹣∠OCB=180°﹣42°﹣42°=96°,
故答案为:96.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,点![]() 在线段
在线段![]() 外,且
外,且![]() ,求证:点
,求证:点![]() 在线段
在线段![]() 的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
A.作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() B.过点
B.过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C.取![]() 中点
中点![]() ,连接
,连接![]() D.过点
D.过点![]() 作
作![]() ,垂足为
,垂足为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
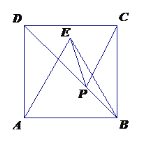
【题目】如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
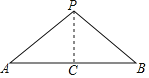
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳远运动员李阳对训练效果进行测试.6次跳远的成绩如下:7.5,7.7,7.6,7.7,7.9,7.8(单位:m)这六次成绩的平均数为7.7m,方差为![]() .如果李阳再跳一次,成绩为7.7m.则李阳这7次跳远成绩的方差_____(填“变大”、“不变”或“变小”).
.如果李阳再跳一次,成绩为7.7m.则李阳这7次跳远成绩的方差_____(填“变大”、“不变”或“变小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
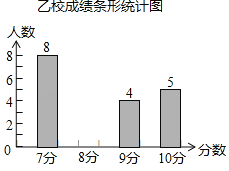
【题目】甲、乙两校参加学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分),乙校平均分是8.3分,乙校的中位数是8分.依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图;
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | ■ | 8 |
(1)请你将乙校成绩统计图直接补充完整;
(2)请直接写出甲校的平均分是 ,甲校的中位数是 ,甲校的众数是 ,从平均分和中位数的角度分析 校成绩较好(填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市第一次用![]() 元购进甲、乙两种商品,其中甲商品件数的
元购进甲、乙两种商品,其中甲商品件数的![]() 倍比乙商品件数的
倍比乙商品件数的![]() 倍多
倍多![]() 件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
甲 | 乙 | |
进价(元/件) | 20 | 28 |
售价(元/件) | 26 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、 乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的![]() 倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多
倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多![]() 元,则第二次乙商品是按原价打几折销售的?
元,则第二次乙商品是按原价打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com