
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

【答案】(1)证明见解析;(2)四边形AFBE是菱形.
【解析】
试题分析:(1)由平行四边形的性质得出AD∥BC,得出∠AEG=∠BFG,由AAS证明△AGE≌△BGF即可;
(2)由全等三角形的性质得出AE=BF,由AD∥BC,证出四边形AFBE是平行四边形,再根据EF⊥AB,即可得出结论.
试题解析:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEG=∠BFG,∵EF垂直平分AB,∴AG=BG,在△AGEH和△BGF中,∵∠AEG=∠BFG,∠AGE=∠BGF,AG=BG,∴△AGE≌△BGF(AAS);
(2)解:四边形AFBE是菱形,理由如下:
∵△AGE≌△BGF,∴AE=BF,∵AD∥BC,∴四边形AFBE是平行四边形,又∵EF⊥AB,∴四边形AFBE是菱形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒
交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.

(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数1,1,2,3,5,8,13是“斐波那契数列”的一部分,若去掉其中的两个数后这组数的中位数、众数保持不变,则去掉的两个数是( )
A.2,5B.1,2C.2,3D.5,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家购进A、B两种商品,A种商品用了480元,B种商品用了1260元,A、B两种商品的数量比为1﹕3,A种商品每千克的进价比B种商品每千克的进价多2元.A、B两种商品各购进多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
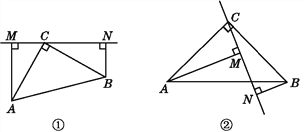
(1)试说明:MN=AM+BN.
(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查全校七年级学生 每天(除课间操外)的课外锻炼时间。
(1)确定调查方式时,甲说:“我到(1)班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到全校七年级每个班去随机调查一定数量的同学”。你认为调查方式最合理的是(填“甲”、或“乙”或“丙”)_________
(2)他们采用了最为合适的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将两幅统计图补充完整;


(3)若该七年级共有1200名同学,请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com