
【题目】如图,抛物线![]() 交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒
交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.

【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)当t1=
;(3)当t1=![]() 秒,此时路径长度为
秒,此时路径长度为![]() ,当t2=5秒,此时路径长度为
,当t2=5秒,此时路径长度为![]() .
.
【解析】试题分析:(1)利用待定系数法求二次函数的解析式;
(2)先表示G的坐标,再把点G的坐标代入抛物线的解析式中列方程可得t的值;
(3)如图2,先计算当G在BD上时,t的值;
分三种情况进行讨论:
①当0≤t≤![]() 时,如图3,作辅助线,根据S△BCG=S梯形GHDB+S△BDC﹣S△GHC,列式可得t的值,利用勾股定理求AG的长即可;
时,如图3,作辅助线,根据S△BCG=S梯形GHDB+S△BDC﹣S△GHC,列式可得t的值,利用勾股定理求AG的长即可;
②当G在BC上时,如图4,根据同角的三角函数得tan∠C=![]() =2,则GH=2HC,列关于t的方程得:t=
=2,则GH=2HC,列关于t的方程得:t=![]() ;当
;当![]() <t≤
<t≤![]() 时,如图5,同理可得结论;
时,如图5,同理可得结论;
③当E与D重合时,F与B重合,如图6,此时t=4,计算此时△BCG的面积为2,因此点G继续向前运动;
当t>4时,如图7,同理列方程可得结论.
试题解析:解:(1)将B(4,4)和C(6,0)代入抛物线![]() 得:
得: ![]() ,解得:
,解得:  ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() ;
;
(2)如图1,由题意得:AE=![]() t,∵A(0,4),B(4,4),∴AB⊥y轴,且AB∥x轴,∵OA=OD=4,∴△AOD是等腰直角三角形,∴∠ADO=∠BAD=45°,∴△AFE是等腰直角三角形,∴AF=EF=t,∵△EFG是等腰直角三角形,∴G(t+
t,∵A(0,4),B(4,4),∴AB⊥y轴,且AB∥x轴,∵OA=OD=4,∴△AOD是等腰直角三角形,∴∠ADO=∠BAD=45°,∴△AFE是等腰直角三角形,∴AF=EF=t,∵△EFG是等腰直角三角形,∴G(t+![]() t,4﹣
t,4﹣![]() t),即:点G(
t),即:点G(![]() t,4﹣
t,4﹣![]() t),将点G(
t),将点G(![]() t,4﹣
t,4﹣![]() t)代入到抛物线得: 4﹣
t)代入到抛物线得: 4﹣![]() t=
t=![]() ,解得:t1=0(舍),t2=
,解得:t1=0(舍),t2=![]() .
.
答:当t=![]() 时,点G落在抛物线上;
时,点G落在抛物线上;
(3)如图2,连接BD,当G在BD上时, ![]() t=4,t=
t=4,t=![]() ,分三种情况讨论:
,分三种情况讨论:
①当0≤t≤![]() 时,如图3,过G作GH⊥x轴于H,延长HG交AB于M,则GM⊥AB,∵B(4,4),D(4,0),∴BD⊥x轴,∴S△BCG=S梯形GHDB+S△BDC﹣S△GHC,4=
时,如图3,过G作GH⊥x轴于H,延长HG交AB于M,则GM⊥AB,∵B(4,4),D(4,0),∴BD⊥x轴,∴S△BCG=S梯形GHDB+S△BDC﹣S△GHC,4=![]() (4﹣
(4﹣![]() t+4)(4﹣
t+4)(4﹣![]() t)+
t)+![]() ×4×(6﹣4)﹣
×4×(6﹣4)﹣![]() (6﹣
(6﹣![]() t)(4﹣
t)(4﹣![]() t),4=
t),4=![]() t,解得:t=
t,解得:t=![]() ,∴AM=
,∴AM=![]() t =
t =![]() ×
×![]() =
=![]() ,GM=
,GM=![]() t=
t=![]() ×
×![]() =
=![]() ,在Rt△AGM中,由勾股定理得:AG=
,在Rt△AGM中,由勾股定理得:AG=![]() =
= =
=![]() ;
;
∴当t=![]() 时,此时点G运动的路径长为
时,此时点G运动的路径长为![]() ;
;
②当G在BC上时,如图4,tan∠C=![]() =2,∴GH=2HC,∴4﹣
=2,∴GH=2HC,∴4﹣![]() t=2(6﹣
t=2(6﹣![]() t),t=
t),t=![]() ,当
,当![]() <t≤
<t≤![]() 时,如图5,S△BCG=S△BDC﹣S梯形BDHG﹣S△GHC,4=
时,如图5,S△BCG=S△BDC﹣S梯形BDHG﹣S△GHC,4=![]() ×4×2﹣
×4×2﹣![]() (4﹣
(4﹣![]() t+4)(
t+4)(![]() t﹣4)﹣
t﹣4)﹣![]() ×(4-
×(4-![]() t)(6-
t)(6-![]() t),t=
t),t=![]() (不在此范围内,不符合题意);
(不在此范围内,不符合题意);
③当E与D重合时,F与B重合,如图6,t=![]() =4,∴G(6,2),∴AG=
=4,∴G(6,2),∴AG=![]() =
=![]() ,∴S△BCG=S梯形BDCG﹣S△BDC=
,∴S△BCG=S梯形BDCG﹣S△BDC=![]() ×2×(4+2)﹣
×2×(4+2)﹣![]() ×2×4=2,∴当t>4时,如图7,由题意得:DE=t﹣4,∴OE=t﹣4+4=t,∴OH=OE+EH=t+2,EH=2,GM=GH=2,BM=t+2﹣4=t﹣2,CH=t+2﹣6=t﹣4,过G作MH⊥x轴,交x轴于H,交直线AB于M,∴S△BGC=S梯形BCHM﹣S△BGM﹣S△GCH,4=
×2×4=2,∴当t>4时,如图7,由题意得:DE=t﹣4,∴OE=t﹣4+4=t,∴OH=OE+EH=t+2,EH=2,GM=GH=2,BM=t+2﹣4=t﹣2,CH=t+2﹣6=t﹣4,过G作MH⊥x轴,交x轴于H,交直线AB于M,∴S△BGC=S梯形BCHM﹣S△BGM﹣S△GCH,4=![]() (t﹣4+t﹣2)×4﹣
(t﹣4+t﹣2)×4﹣![]() ×2×(t﹣2)﹣
×2×(t﹣2)﹣![]() ×2×(t﹣4),t=5,当t=5时,点G的运动路径分为两部分组成:
×2×(t﹣4),t=5,当t=5时,点G的运动路径分为两部分组成:
i)点G从A运动到D时,运动路径为:如图6中的AG长,即为![]() ;
;
ii)点G从D点继续在射线DC上运动1秒时,路径为1;
所以当t=5时,此时点G运动的路径长度为![]() .
.
综上所述:当t1=![]() 秒,此时路径长度为
秒,此时路径长度为![]() ,当t2=5秒,此时路径长度为
,当t2=5秒,此时路径长度为![]() .
.





科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵ ∠1 =∠2 (已知)
∴ ∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
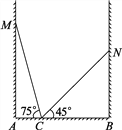
【题目】如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com