
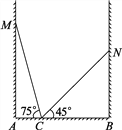
【题目】如图,房间内有一架梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,若梯子斜靠在另一面墙时,顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这个房间的宽AB是多少米?为什么?
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用120元钱按批发价从蔬菜批发市场买了西红柿和豆角共40kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.4 | 3.2 |
零售价(单位:元/kg) | 3.8 | 5.2 |
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么只需要测量______才能测得A、B之间的距离,依据是:__________________________________________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒
交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点E从点A出发,以每秒![]() 个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
个单位长度的速度沿线段AD向点D运动,到达点D后,以每秒1个单位长度的速度沿射线DC运动,设点E的运动时间为t秒,过点E作AB的垂线EF交直线AB于点F,以线段EF为斜边向右作等腰直角△EFG.
(1)求抛物线的解析式;
(2)当点G落在第一象限内的抛物线上时,求出t的值;
(3)设点E从点A出发时,点E,F,G都与点A重合,点E在运动过程中,当△BCG的面积为4时,直接写出相应的t值,并直接写出点G从出发到此时所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.

(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com