Question

【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.

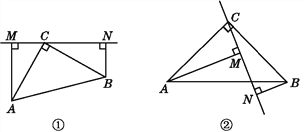
(1)试说明:MN=AM+BN.

(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.

Answer 1

【答案】(1) 答案见解析;(2) 不成立

【解析】试题分析：（1）利用互余关系证明∠MAC=∠NCB，又∠AMC=∠CNB=90°，AC=BC，故可证△AMC≌△CNB，从而有AM=CN，MC=BN，即可得出结论；

（2）类似于（1）的方法，证明△AMC≌△CNB，从而有AM=CN，MC=BN，可推出AM、BN与MN之间的数量关系．

试题解析：解：（1）∵AM⊥MN，BN⊥MN，∴∠AMC=∠CNB=90°．

∵∠ACB=90°，∴∠MAC+∠ACM=90°，∠NCB+∠ACM=90°，∴∠MAC=∠NCB．

在△AMC和△CNB中，∵∠AMC＝∠CNB，∠MAC＝∠NCB，AC＝CB，∴△AMC≌△CNB（AAS），∴AM=CN，MC=NB．

∵MN=NC+CM，∴MN=AM+BN；

（2）图（1）中的结论不成立，MN=BN-AM．理由如下：

∵AM⊥MN，BN⊥MN，∴∠AMC=∠CNB=90°．

∵∠ACB=90°，∴∠MAC+∠ACM=90°，∠NCB+∠ACM=90°，∴∠MAC=∠NCB．

在△AMC和△CNB中，∵∠AMC＝∠CNB，∠MAC＝∠NCB，AC＝CB，∴△AMC≌△CNB（AAS），∴AM=CN，MC=NB．

∵MN=CM-CN，∴MN=BN-AM．