
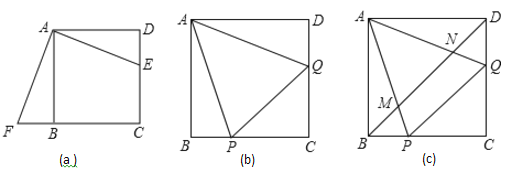
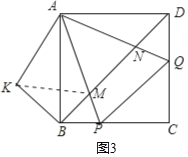
【题目】在正方形![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,
(1)将![]() 绕点
绕点![]() 按顺时针方向旋转。使
按顺时针方向旋转。使![]() 、
、![]() 重合,得到
重合,得到![]() ,如图(a)所示.观察可知:与
,如图(a)所示.观察可知:与![]() 相等的线段是__________,
相等的线段是__________,![]() __________.
__________.
(2)如图(b)所示,正方形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,且
边上的点,且![]() ,试通过旋转的方式说明:
,试通过旋转的方式说明:![]() .
.
(3)在(2)的条件下,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,如图(c)所示.判断
,如图(c)所示.判断![]() 、
、![]() 、
、![]() 之间的关系,直接写出结论.
之间的关系,直接写出结论.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
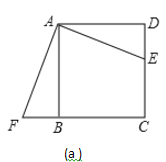
(1)如图(a),直接根据旋转的性质得到DE=BF,∠AFB=∠AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;
(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBK=∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2,然后利用等相等代换即可得到BM2+DN2=MN2.
(1)如图(a).
∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF.
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中,
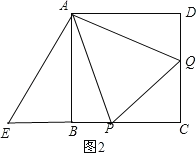
∵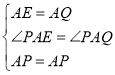 ,
,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ;
(3)BM2+DN2=MN2.证明如下:
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图3,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK.
∵∠MBK=∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.


科目:初中数学 来源: 题型:
【题目】2019年10月1日,中华人民共和国70年华诞之际,王梓涵和学校国旗护卫队的其他同学们赶到学校举行了简朴而降重的升旗仪式.倾听着雄壮的国歌声,目送着五星红旗级缓升起,不禁心潮澎湃,爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高度.将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端2米,然后将绳子末端拉直到距离旗杆5m处,测得此时绳子末端距离地面高度为1m,最后根据刚刚学习的勾股定理就能算出旗杆的高度为( )
A.10mB.11mC.12mD.13m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毎年6月,学校门口的文具店都会购进毕业季畅销商品进行销售.已知校门口“小光文具店“在5月份就售出每本8元的A种品牌同学录90本,每本10元的B种品牌同学录175本.
(1)某班班长帮班上同学代买A种品牌和B种品牌同学录共27本,共花费246元,请问班长代买A种品牌和B种品牌同学录各多少本?
(2)该文具店在6月份决定将A种品牌同学录每本降价3元后销售,B种品牌同学录每本降价a%(a>0)后销售.于是,6月份该文具店A种品牌同学录的销量比5月份多了![]() a%,B种品牌同学录的销量比5月份多了(a+20)%,且6月份A、B两种品牌的同学录的销售总额达到了2550元,求a的值.
a%,B种品牌同学录的销量比5月份多了(a+20)%,且6月份A、B两种品牌的同学录的销售总额达到了2550元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
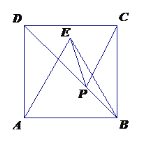
【题目】如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
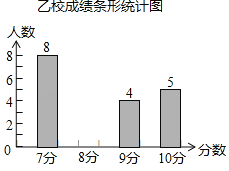
【题目】甲、乙两校参加学生英语口语比赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分),乙校平均分是8.3分,乙校的中位数是8分.依据统计数据绘制了如下尚不完整的甲校成绩统计表和乙校成绩统计图;
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | ■ | 8 |
(1)请你将乙校成绩统计图直接补充完整;
(2)请直接写出甲校的平均分是 ,甲校的中位数是 ,甲校的众数是 ,从平均分和中位数的角度分析 校成绩较好(填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下空隙,又不互相重叠(在几何里叫作平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请根据下列图形,填写表中空格.

(2)如图所示,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形.
(3)不能用正五边形形状的材料铺满地面的理由是什么?
(4)从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com